The difference between the time taken by two buses to travel a distance of 350 km is 2 hours 20 minutes. If the difference between their speeds is 5 kmph, find the slower speed.
35 kmph
30 kmph
25 kmph
20 kmph
The correct Answer is:C
To solve the problem step by step, we will follow these steps:
Step 1: Define Variables
Let the speed of the faster bus be V1 km/h and the speed of the slower bus be V2 km/h.
Step 2: Set Up the First Equation
According to the problem, the difference between their speeds is given as:
V1−V2=5(Equation 1)
Step 3: Convert Time Difference
The difference in time taken by the two buses to travel 350 km is given as 2 hours and 20 minutes. We convert this into hours:
2 hours 20 minutes=2+2060=2+13=73 hours
Step 4: Set Up the Second Equation
The time taken by the faster bus to cover 350 km is:
T1=350V1
The time taken by the slower bus to cover the same distance is:
T2=350V2
According to the problem, the difference in time taken is:
T2−T1=73
Substituting for T1 and T2:
350V2−350V1=73(Equation 2)
Step 5: Simplify Equation 2
Multiply through by V1×V2 to eliminate the denominators:
350V1−350V2=73V1V2
Step 6: Rearranging the Equation
Rearranging gives:
350(V1−V2)=73V1V2
Step 7: Substitute Equation 1 into the Rearranged Equation
From Equation 1, we know V1−V2=5:
350×5=73V1V2
1750=73V1V2
Step 8: Solve for V1V2
Multiply both sides by 3:
5250=7V1V2
Now divide by 7:
V1V2=750(Equation 3)
Step 9: Substitute V1 in terms of V2
From Equation 1, we have:
V1=V2+5
Substituting into Equation 3:
(V2+5)V2=750
V22+5V2−750=0
Step 10: Solve the Quadratic Equation
Now we can solve the quadratic equation:
Using the quadratic formula V2=−b±√b2−4ac2a:
Here, a=1,b=5,c=−750:
V2=−5±√52−4⋅1⋅(−750)2⋅1
V2=−5±√25+30002
V2=−5±√30252
V2=−5±552
Calculating the two potential solutions:
1. V2=502=25 (valid speed)
2. V2=−602=−30 (not valid)
Conclusion
Thus, the slower speed V2 is:
V2=25 km/h
Let the speed of the faster bus be V1 km/h and the speed of the slower bus be V2 km/h.
According to the problem, the difference between their speeds is given as:
V1−V2=5(Equation 1)
The difference in time taken by the two buses to travel 350 km is given as 2 hours and 20 minutes. We convert this into hours:
2 hours 20 minutes=2+2060=2+13=73 hours
The time taken by the faster bus to cover 350 km is:
T1=350V1
T2=350V2
T2−T1=73
Substituting for T1 and T2:
350V2−350V1=73(Equation 2)
Multiply through by V1×V2 to eliminate the denominators:
350V1−350V2=73V1V2
Rearranging gives:
350(V1−V2)=73V1V2
From Equation 1, we know V1−V2=5:
350×5=73V1V2
1750=73V1V2
Multiply both sides by 3:
5250=7V1V2
Now divide by 7:
V1V2=750(Equation 3)
From Equation 1, we have:
V1=V2+5
Substituting into Equation 3:
(V2+5)V2=750
V22+5V2−750=0
Now we can solve the quadratic equation:
Using the quadratic formula V2=−b±√b2−4ac2a:
Here, a=1,b=5,c=−750:
V2=−5±√52−4⋅1⋅(−750)2⋅1
V2=−5±√25+30002
V2=−5±√30252
V2=−5±552
1. V2=502=25 (valid speed)
2. V2=−602=−30 (not valid)
Thus, the slower speed V2 is:
V2=25 km/h
Topper's Solved these Questions
Similar Questions
The speeds of three buses are in the ratio 2:3: 4. The time taken by these buses to travel the same distance will be in the ratio
View SolutionA steamer goes downstream and covers the distance between two ports in 5 hours while it covers the same distance upstream in 6 hours. If the speed of the stream is 1 km/hr, find the speed of the steamer in still water.
View Solution
Knowledge Check
The ratio between the speeds of two trains is, 2 : 5. If the first train runs 350 km in 5 h. then the difference between the speeds (in km/h) of both the trains is :
A75B180C65D105A man has to travels a distance of 20 km. After 1 hour 40 minutes, he observes that the ratio of the covered distance to the remained distance is 5/7. Find the speed of the man
A3 km/hB4 km/hC5 km/hD6 km/hA car travelling at 38 th of its usual speed covers a distance of 65 km in 2 hours 10 minutes. Find the usual speed of car.
A80km/hrB40km/hC160 km/hD120 km/h
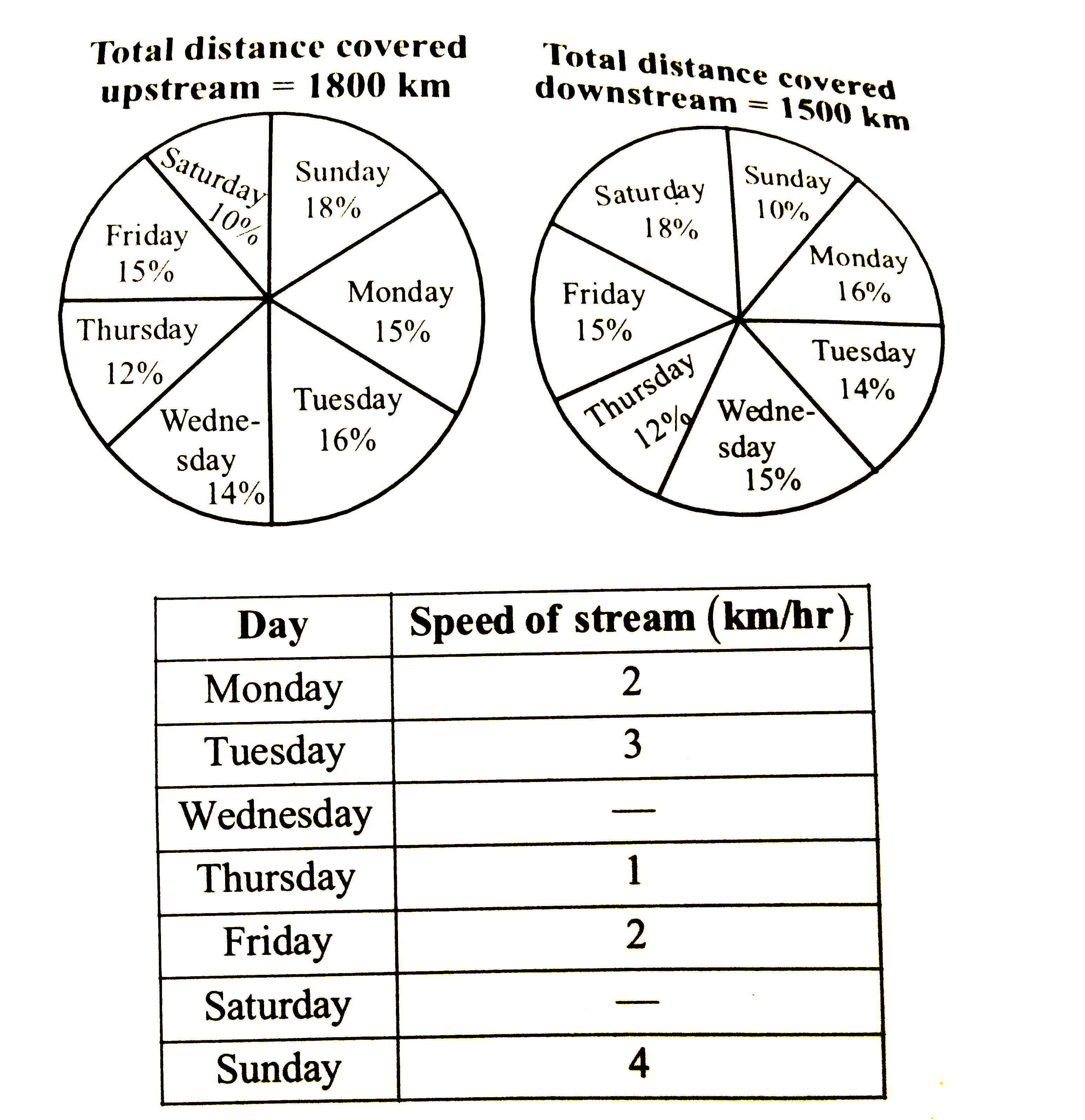
If the time taken by boat to travel upstream on Sunday is 2 hours more than the time takeb by it to travel downstream on Thursday and the speed of boat in still water on Thursday is 17 kmph, then find the upstream speed of boat on Sunday ?
View SolutionA steamer goes downstream and covers distance between two ports in 4 hours, while it covers the same distance upstream in 5 hours. If the speed of the stream is 2 km/h, then find the speed of the streamer in still water.
View SolutionAmit travels 30 minutes at the speed of 25 km/hr. Further he travels 20 minutes at the speed of 40 km/hr. Find his average speed.
View SolutionRatio between speed of yatch in still water to speed of stream is 8:1.if 67.5km is travelled downstream in 2.5 hours then find the differenec between speed of yatch in still water to speed of strem (in kmph)?
View SolutionThe speed of the boat in still water is 24 km\h and the speed of the stream is 4 km/h .The time taken by the boat to travel from A to B downstream is 36 minutes less than the time taken by the same boat to travel from B to C upstream .If the distance between A and B is 4 km more than the distance between B and C , what is the distance between A and B ?
View Solution
