3162162 find R.
0
1
2
3
The correct Answer is:81
To find the remainder R when 3162162 is calculated, we can follow these steps:
1. Understand the Problem: We need to find the remainder R when 3162 is divided by 162.
2. Factor 162: The first step is to factor 162:
162=2×81=2×34
3. Use the Chinese Remainder Theorem: Since 162 can be expressed as 2×34, we can find the remainders of 3162 modulo 2 and 81 separately.
4. Calculate 3162mod2:
3≡1mod2
Therefore,
3162mod2≡1162≡1
5. Calculate 3162mod81:
Since 81=34, we can directly see that:
3162≡0mod81
6. Combine the Results: We have:
3162≡1mod2
3162≡0mod81
7. Finding the Common Solution: We need to find a number x such that:
x≡0mod81
x≡1mod2
The numbers that satisfy x≡0mod81 are 0,81,162,…. Among these, the only number that is odd (to satisfy x≡1mod2) is 81.
8. Conclusion: Therefore, the remainder R when 3162 is divided by 162 is:
R=81
162=2×81=2×34
3≡1mod2
Therefore,
3162mod2≡1162≡1
Since 81=34, we can directly see that:
3162≡0mod81
3162≡1mod2
3162≡0mod81
x≡0mod81
x≡1mod2
R=81
Topper's Solved these Questions
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - NUMBER SYSTEM EXERCISE - MULTIPLE CHOICE QUESTIONS225videos
NUMBER SYSTEM
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - MOCK TEST IIEXERCISE - MCQ100videos
MOCK TEST II
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - PARTNERSHIPEXERCISE - Questions26videos
PARTNERSHIP
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the remainder when (3)162 is divided by 162.
A1B81C150D100 - Question 2 - Select One
The value of (27)n/3×(8)−n/6(162)−n/2 is equal to
A2nB3nC33nD35n
If the position vectors of P and Q are ˆi+2ˆj−7ˆk and 5ˆi−3ˆj+4ˆk them the cosine of the angle between →PQ and y-axis is 5√162 b. 4√162 c. −5√162 d. 11√162
View SolutionThe rational expression 2x4−162(x2+9)(2x−6) in its lowest terms is:
View SolutionThe solution of the equation 5xlog23+3log2x=162 is
View SolutionA ray of light is incident on a transparent glass slab of refractive index 1.62. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence ? [tan–1(1.62)=58.3∘]
View SolutionIn the figure, P is the point of contact.
If OP=7.2,OR=16.2, find QR.
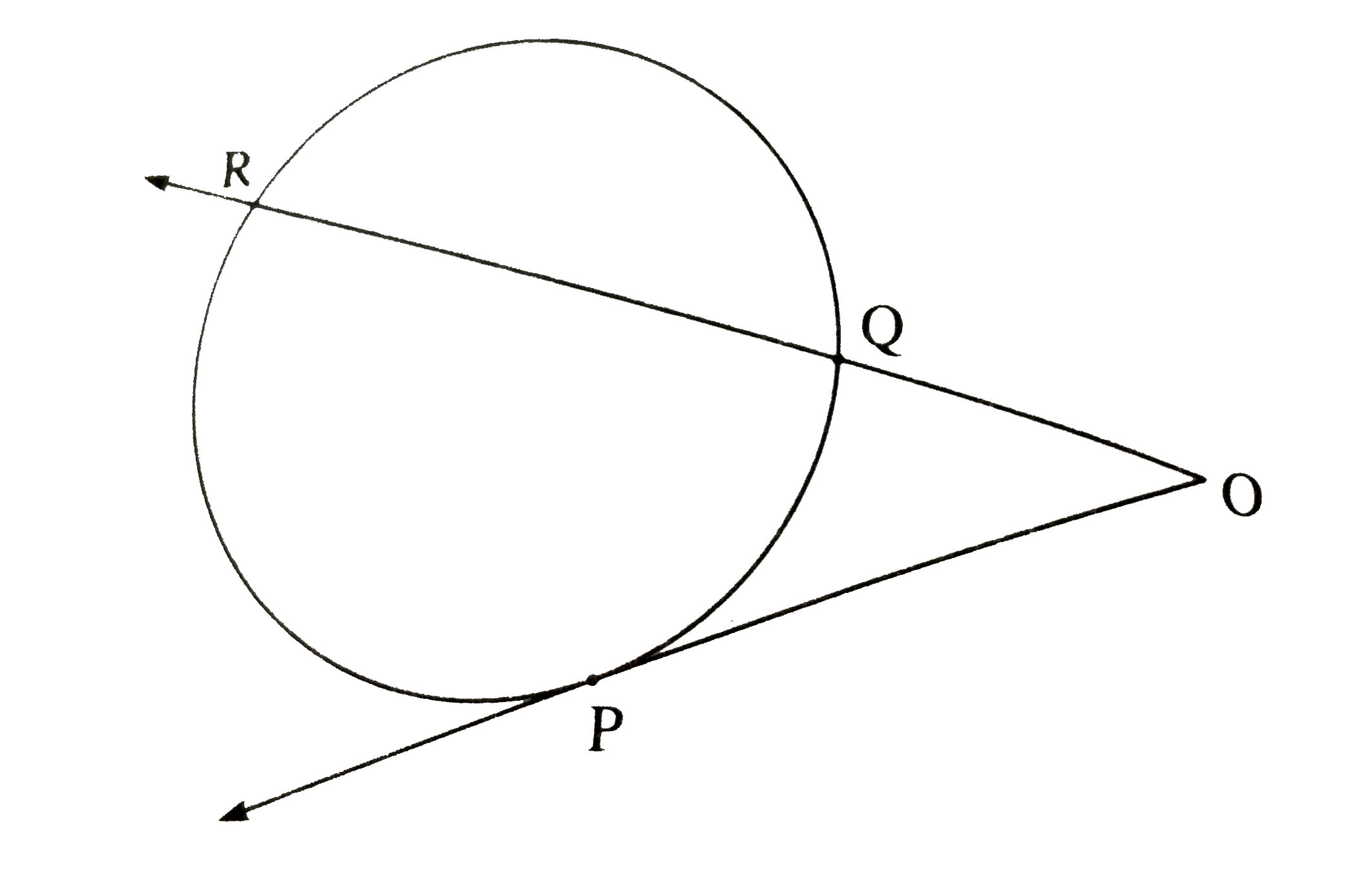 View Solution
View SolutionCalculate the weight of CaO required to remove hardness of 106L of water containing 1.62g of Ca(HCO3)2 in 1.0L.
(MwofCa(HCO3)2=162,mwofCaO=56)View Solution

