how many zeroes in 60!
To find the number of trailing zeros in 60!, we can use the formula that counts how many times 5 is a factor in the numbers from 1 to 60. This is because the number of trailing zeros in a factorial is determined by the number of pairs of factors of 2 and 5, and there are always more factors of 2 than 5.
1. Identify the formula: The number of trailing zeros in n! can be calculated using the formula:
Number of trailing zeros=⌊n5⌋+⌊n52⌋+⌊n53⌋+…
until 5k>n.
2. Calculate for n=60:
- First, calculate ⌊605⌋:
⌊605⌋=⌊12⌋=12
- Next, calculate ⌊6025⌋:
⌊6025⌋=⌊2.4⌋=2
- Now, calculate ⌊60125⌋:
⌊60125⌋=⌊0.48⌋=0
- Since 125>60, we stop here.
3. Add the results:
Total trailing zeros=12+2+0=14
Final Answer:
Thus, the number of trailing zeros in 60! is 14.
---
Number of trailing zeros=⌊n5⌋+⌊n52⌋+⌊n53⌋+…
until 5k>n.
- First, calculate ⌊605⌋:
⌊605⌋=⌊12⌋=12
- Next, calculate ⌊6025⌋:
⌊6025⌋=⌊2.4⌋=2
- Now, calculate ⌊60125⌋:
⌊60125⌋=⌊0.48⌋=0
- Since 125>60, we stop here.
Total trailing zeros=12+2+0=14
Thus, the number of trailing zeros in 60! is 14.
Similar Questions
Knowledge Check
How many zeroes will be there for the polynomial f(x) = (x−2)2 + 4?
A0B1C2D3How many zeroes will be there for the polynomial f(x)=(x−2)2+4 ?
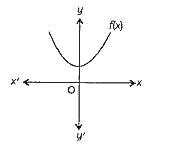
A0B1C2D3How many zeroes and there of y = f(x) for the given graph?
 A0B1C2D3
A0B1C2D3