210653 Find R .
To find the remainder R when 210653, we can follow these steps:
Step 1: Rewrite the expression
We start with the expression 210653. We can express 2106 in terms of 4 (since 4=22):
2106=(22)53⋅20=453
Step 2: Apply Fermat's Little Theorem
Since 4 and 53 are coprime (they have no common factors other than 1), we can use Fermat's Little Theorem, which states that if p is a prime and a is an integer not divisible by p, then:
ap−1≡1modp
Here, p=53 and a=4. According to Fermat's theorem:
452≡1mod53
Step 3: Simplify 453
Now we can express 453 as:
453=452⋅4≡1⋅4mod53
Thus:
453≡4mod53
Step 4: Conclusion
The remainder R when 2106 is divided by 53 is:
R=4
Final Answer
The remainder R is 4.
---
We start with the expression 210653. We can express 2106 in terms of 4 (since 4=22):
2106=(22)53⋅20=453
Since 4 and 53 are coprime (they have no common factors other than 1), we can use Fermat's Little Theorem, which states that if p is a prime and a is an integer not divisible by p, then:
ap−1≡1modp
Here, p=53 and a=4. According to Fermat's theorem:
452≡1mod53
Now we can express 453 as:
453=452⋅4≡1⋅4mod53
Thus:
453≡4mod53
The remainder R when 2106 is divided by 53 is:
R=4
The remainder R is 4.
Similar Questions
Knowledge Check
A(-11,7) and B (-10,6) are the points of trisection of a line segment PQ . Find the coordinates of P and Q .
A(−12,8),(−9,5)B(−12,−8),(−9,5)C(12,0) , (9 ,-5)D(12 , -8) , ( 9 , -5)(4.53−3.07)2(3.07−2.15)(2.15−4.53)+(3.07−2.15)2(2.15−4.53)(4.53−3.07)+(2.15−4.53)2(4.53−3.07)(3.07−2.15) is simplified to
A0B1C2D3
If a + b = 9 and a2+b2=53, then find the value of ab
View Solutionprove that (106)85−(85)106 is divisible by 7
View Solution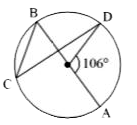
In the above figure the centre of the circle is O and ∠AOD=106∘ then find ∠BCD.
View SolutionThe coordinates of the initial point of a vector are (2,3) and those of the terminal point are (10,6).Find the magnitude and direction of the vector.
View SolutionLet A={2,3,4,5} R={(2, 2),and let R(3,3),(4,4),(5,5),(2,3),(3,2)(3,5),(5,3)} be a relation on A. Then R is
View SolutionAn AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term.
View Solution