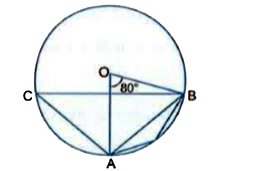
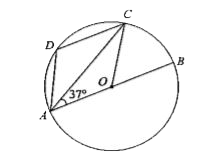
A,B,C and D are 4 points on the circumference of the circle and O is the centre of circle ∠OBD−∠CBD=∠BDC−∠ODB find ∠A
A
60∘
B
50∘
C
72∘
D
120∘
Video Solution
|
Answer
Step by step video & image solution for A,B,C and D are 4 points on the circumference of the circle and O is the centre of circle angle OBD - angle CBD = angle BDC - angle ODB find angle A by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If O is the centre of circle and ∠ADE=60∘ then find ∠AOC
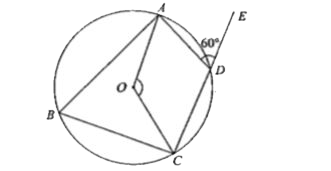 A60∘B100∘C120∘DNone of these
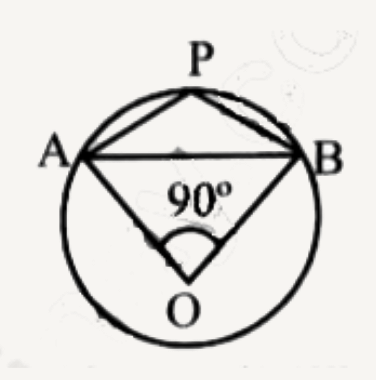
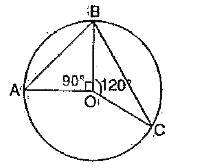
A60∘B100∘C120∘DNone of theseO is the centre of a circle ∠AOB=90∘and∠BOC=120∘.∠ABC is equal to
 A150∘B210∘C75∘D105∘
A150∘B210∘C75∘D105∘In the figure, O is the centre of the circle . ∠PQR is equal to
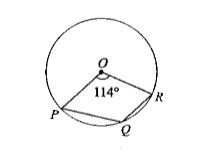 A57∘B63∘C123∘D92∘
A57∘B63∘C123∘D92∘
In the given figure of circle, ‘O’ is the centre of the circle ∠AOB=130∘. What is the value of ∠DMC?
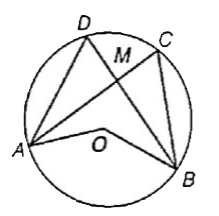
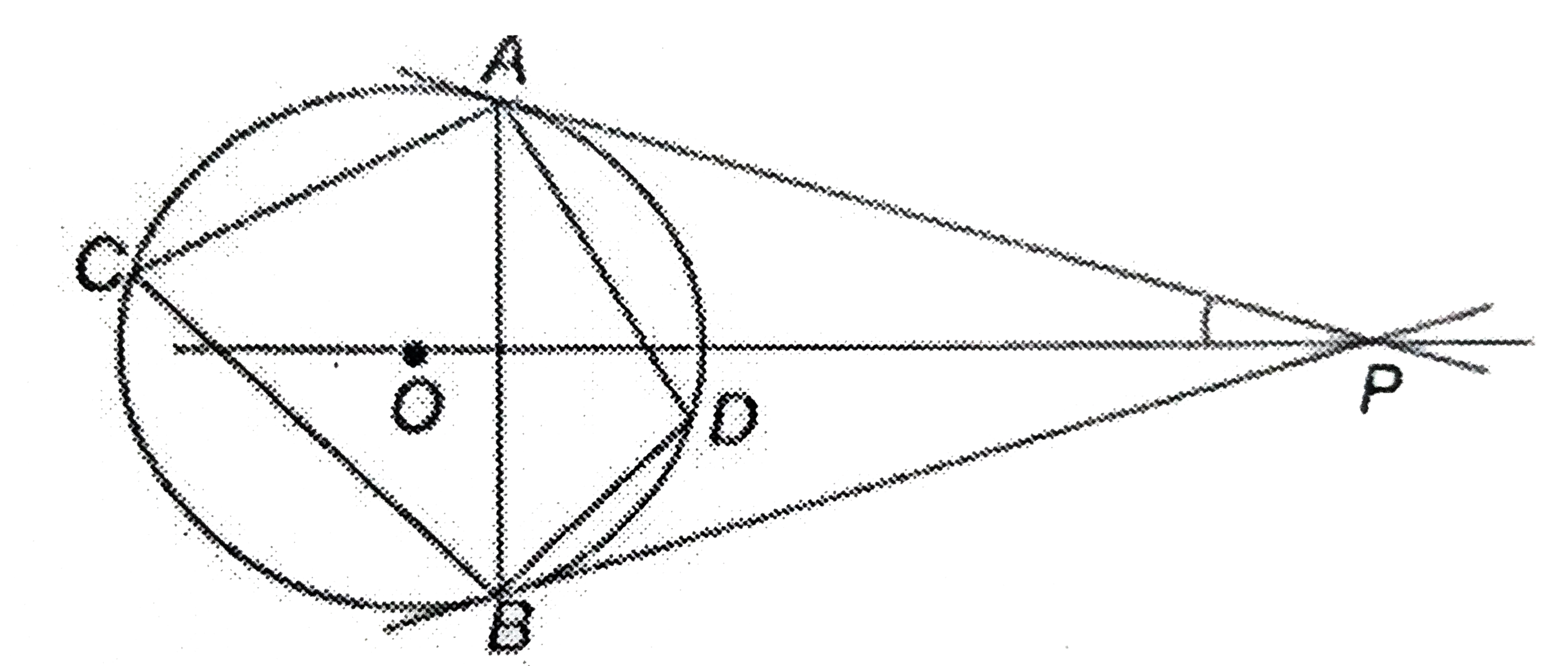
View SolutionIn the diagram , O is the centre of the circle and ∠OPA=30∘, Find ∠ACBand∠ADB respectively.
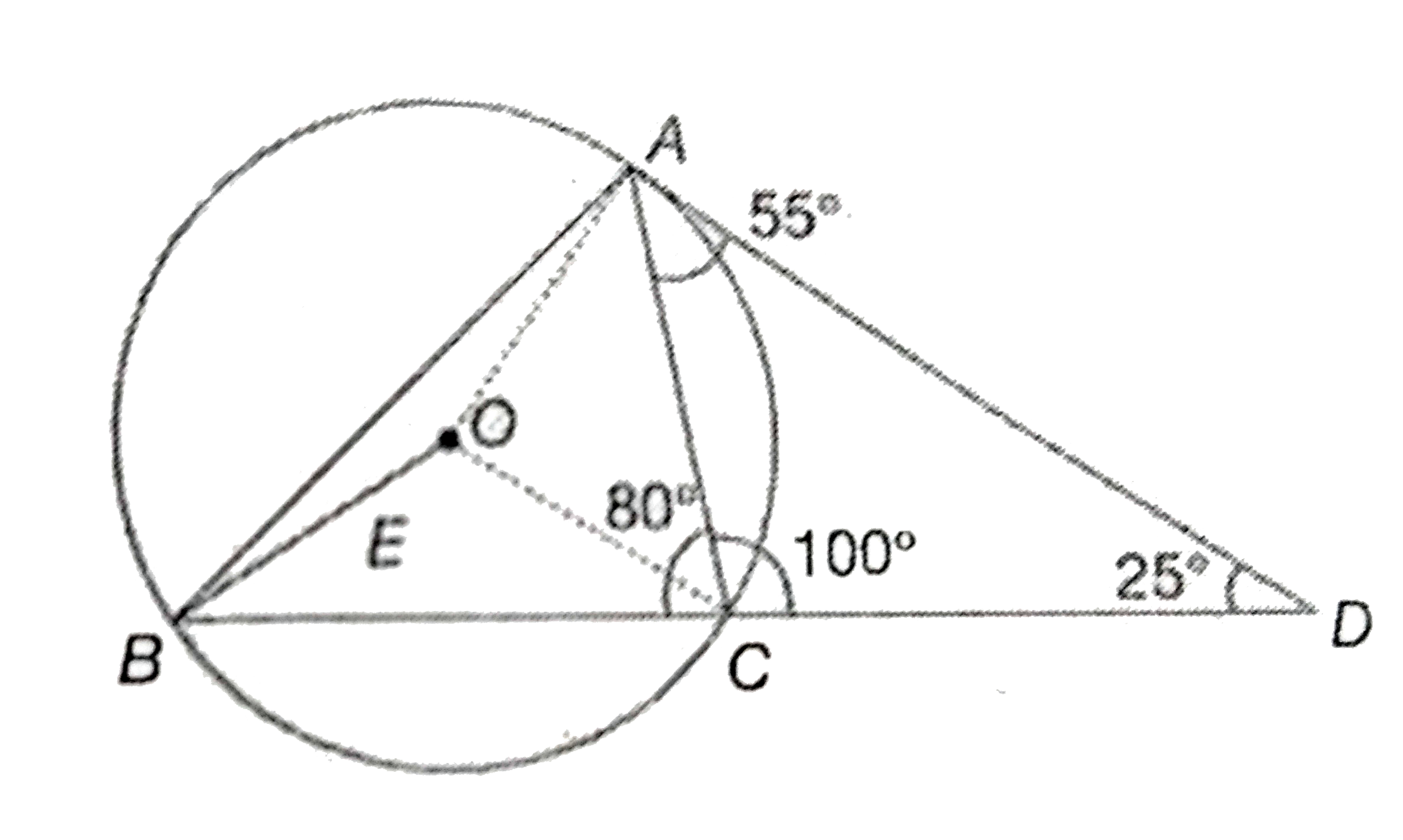
View SolutionIn the given, figure , O is the centre of the circle and AD is a tangent to the circle at.A if ∠CAD=55∘ and ∠ADC=25∘, then find ∠ABO.
View SolutionWhat is the angle ∠AED if O is the centre of the circle?
View SolutionIf O is the centre of the circle then find ∠ADC
View Solution