In a trapezium ABCD, AB and DC are parallel sides and ∠ADC=90∘ . If AB = 15 cm, CD = 40 cm and diagonal AC = 41 cm. Then the area of the trape- zium ABCD is:
245 cm2
240 cm2
247.5 cm2
250 cm2
To find the area of trapezium ABCD where AB and CD are parallel sides, and given the dimensions, we can follow these steps:
Step 1: Identify the given values
- Length of AB (top base) = 15 cm
- Length of CD (bottom base) = 40 cm
- Length of diagonal AC = 41 cm
- Angle ADC = 90 degrees
Step 2: Understand the trapezium configuration
Since angle ADC is 90 degrees, we can visualize triangle ADC where:
- AD is the height of the trapezium.
- CD is the base of the triangle.
- AC is the hypotenuse.
Step 3: Apply the Pythagorean theorem
In triangle ADC, we can use the Pythagorean theorem to find the height AD:
AC2=AD2+CD2
Substituting the known values:
412=AD2+402
Step 4: Calculate the squares
Calculating the squares:
412=1681and402=1600
So we have:
1681=AD2+1600
Step 5: Solve for AD^2
Rearranging the equation gives:
AD2=1681−1600=81
Step 6: Find AD
Taking the square root of both sides:
AD=√81=9 cm
Step 7: Calculate the area of the trapezium
The area A of trapezium ABCD can be calculated using the formula:
A=12×height×(AB+CD)
Substituting the known values:
A=12×9×(15+40)
A=12×9×55
Step 8: Perform the multiplication
Calculating:
A=12×495=247.5 cm2
Final Answer
The area of trapezium ABCD is 247.5 cm2.
---
- Length of AB (top base) = 15 cm
- Length of CD (bottom base) = 40 cm
- Length of diagonal AC = 41 cm
- Angle ADC = 90 degrees
Since angle ADC is 90 degrees, we can visualize triangle ADC where:
- AD is the height of the trapezium.
- CD is the base of the triangle.
- AC is the hypotenuse.
In triangle ADC, we can use the Pythagorean theorem to find the height AD:
AC2=AD2+CD2
Substituting the known values:
412=AD2+402
Calculating the squares:
412=1681and402=1600
So we have:
1681=AD2+1600
Rearranging the equation gives:
AD2=1681−1600=81
Taking the square root of both sides:
AD=√81=9 cm
The area A of trapezium ABCD can be calculated using the formula:
A=12×height×(AB+CD)
Substituting the known values:
A=12×9×(15+40)
A=12×9×55
Calculating:
A=12×495=247.5 cm2
The area of trapezium ABCD is 247.5 cm2.
Topper's Solved these Questions
Similar Questions
In a trapezium ABCD, AB and DC are parallel sides and ∠ADC=90∘,if AB = 15 cm, CD = 40 cm and diagonal AC = 41 cm. Then the area of the trapezium ABCD is
एक समलंब में AB और DC समांतर किनारे है और ∠ADC=90∘ है । यदि AB = 15 से.मी., CD = 40 से.मी. और विकर्ण AC = 41 से.मी. है, तो उस समलंब ABCD का क्षेत्रफल बताइए ।
View SolutionIn the figure. AB and DC are parallel sides of a trapezium ABCD and angle ADC=90∘ given AB=15cm,CD=40cm and diagonal AC=41cm, calculate the area of trapezium ABCD
View Solution
Knowledge Check
In a trapezium ABCD, AB is a parallel to CD. BD is perpendicular to AD. AC is perpendicular to BC. If AD=BC=15cmandAB=25cm, then the area of the trapezium is :
A192cm2B232cm2C172cm2Dnone of theseIn a trapezium ABCD, AB is a parallel to CD. BD is perpendicular to AD. AC is perpendicular to BC. If AD=BC=15cmandAB=25cm, then the area of the trapezium is :
A192cm2B232cm2C172cm2Dnone of the aboveFind the area of a parallelogram ABCD in which AB = 8 cm, BC = 15 cm and diagonal AC = 17 cm.
A220cm2B150cm2C120cm2D175cm2
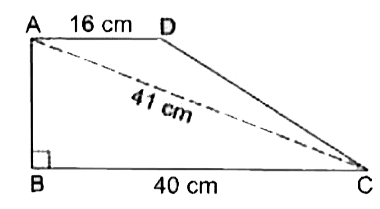
In the given figure, ABCD is a trapezium in which AD∣∣BC,∠ABC=90∘,AD=16cm,AC=41cm and BC = 40 cm. Find the area of the trapezium.
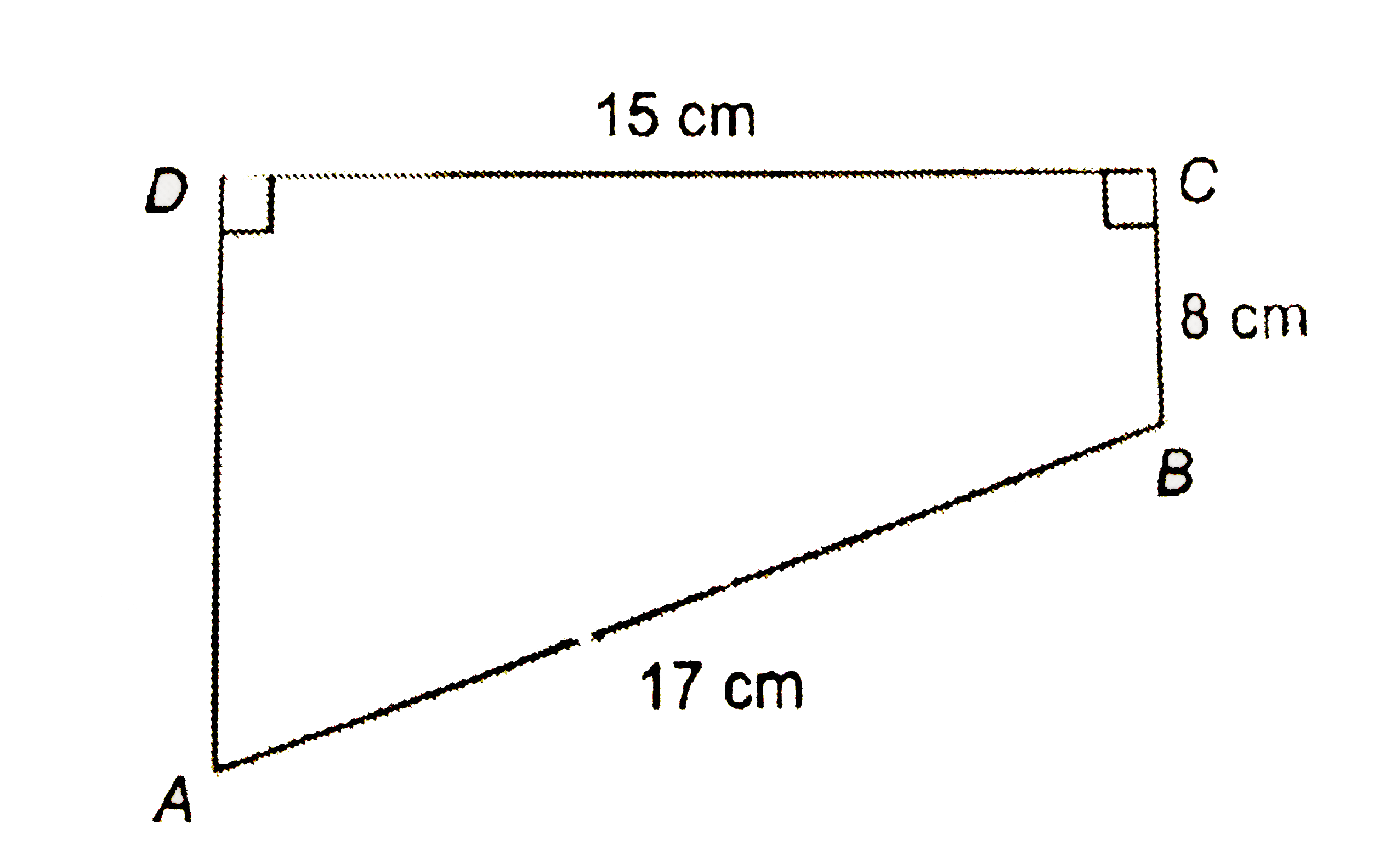
View SolutionThe given figure shows a trapezium ABCD in which AB = 17 cm, BC = 8 cm and CD = 15 cm. Find the area of the trapezium.
View SolutionABCD is a trapezium, where AB is parallel to DC. If AB = 4cm, BC = 3 cm, CD = 7 cm and DA = 2cm, then what is the area of the trapezium?
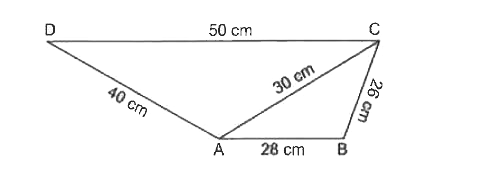
View SolutionIn a quadrilateral ABCD, AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm and diagonal AC = 30 cm. Find the area of the quadrilateral.
View Solution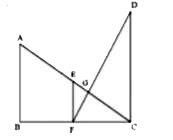
AB, EF and CD are parallel lines. Given that EG = 5 cm, GC = 10 cm, AB = 15 cm and DC = 18 cm, find AC?
View Solution
