A small disk of mass m lies on the highest point of a sphere of radius R. A slight push makes the disk start sliding down. Find the force of pressure of the disk on the sphere as a function of the angle its radius vector makes with the vertical. Where does the disk lose contact with the sphere? Friction is to be neglected.
The correct Answer is:mg(3cosα−2);aret=αrel=arcos23=48∘
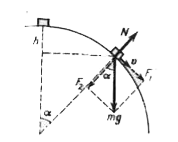
According to Newton.s third law, the pressure of the washer against the sphere is equal in magnitude to the reaction. The forces acting on the object in the direction normal to the velocity vector are the reaction N and the component of the force of gravity F2=mgcosα (see Fig). According to Newton.s second law
F2−N=mv2/R
To find the velocity apply the law of conservation of energy mgh =mv2/2 Since h = (1 — cos ), we obtain after some simple transformations
N=mg(3cosα−2)
When the washwer leaves the sphere it ceases to press against it and the reaction becomes zero. The condition for the loss of contact is cosα=2/3,α=48∘h=R/3
Similar Questions
A particle of mass m is released on a fixed. Smooth sphere of radius R at a position, where the radius through the particle makes an angle of α with the verticle. What is the angle made by radius through the particle when the particle loses contact with sphere? (cosα=3/4)
View SolutionA small box of mass m is placed on the outer surface of a smooth fixed sphere of radius R at a point where the radius makes a angle Pse with the vertical. The box is released from this position. Find the distance travelled by the box before it leaves contact with the sphere.
View Solution
Knowledge Check
A small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?
 A32rB23rC12gt2Dv22g
A32rB23rC12gt2Dv22gA block of mass m is placed on a smooth sphere of radius R. It slides when pushed slightly. At what vertical distance h, from the top, will it leave the sphere?
AR4BR3CR2DRIn figure, a particle is placed at the highest point A of a smooth sphere of radius r. It is given slight push, and it leaves the sphere at B, at a depth h vertically below A. The value of h is
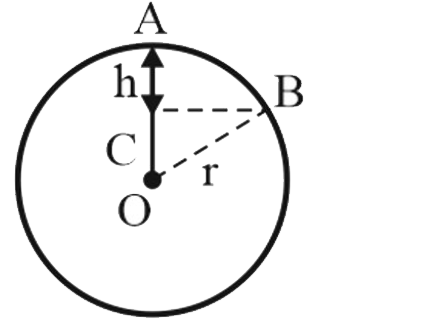 Ar6B14rC13rD12r
Ar6B14rC13rD12r
In figure, a particle is placed at the highest point A of a smooth sphere of radius r. It is given slight push, and it leaves the sphere at B, at a depth h vertically below A. The value of h is

View SolutionA small body A starts sliding off the top of a smooth sphere of radius R. Find the angle θ (figure) corresponding to the point at which the body breaks off the sphere, as well as the break-off velocity of the body.

View SolutionA small mass m starts from rest and slides down the surface of a frictionless solid sphere of radius R. Calculate the angle at which the mass flies off the sphere. If there is friction between the mass and the sphere, does the mass of fly off at a greater or lesser angle than the previous one ?
View SolutionA particle of mass m is kept on a fixed, smooth sphere of radius R at a position, where the radius through the particle makes an angle of 30 ∘ with the vertical. The particle is released from this position. (a) What is the force exerted by the sphere on the particle just after the release? (b) Find the distance traveled by the particle before it leaves contact with the sphere.
View SolutionA motor cycle rides in a hollow sphere in a verticle circle of radius 30 m .What will be the minimum speed required so that he does not lose contact with the surface of sphere at the highest point?
View Solution
