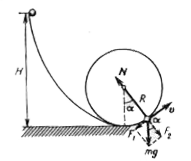
A cyclist rolls down a ''devil's loop'' track from a height H. Find the pressure of the cyclist on the track as a function of the angle the radius vector makes with the vertical. Do the calculations also for the case when the cyclist rolls down from the minimum height.
The correct Answer is:3m(1+cosα)
According to Fig. , we have
N−mgcosα−mv2/R
To find speed apply the law of conservation of energy .
mgH=mgR(1cosα)+mv2/2
Hence
N=mg(3cosα−2+2HR)
In the highest point of the loop α=π , so
Ntop=mg(−5+2HR)
The minimum height is found form the condition Ntop=0 , there fore Hmin=52R. In this case
N=3mg(1+cosα)=6mgcos2α2
Similar Questions
A cyclist goes around a circular track of circumference 410 m in 20 s. Find the angle that his cycle makes with the vertical.
View SolutionA ball rolls down an inclined plane from a height and then goes round a vertical circle of radius 1m. What should be the height of the inclined plane so that the ball is able to go round the circle without leaving the track?
View Solution
Knowledge Check
A solid cylinder rolls down from an inclined plane of height h. What is the velocity of the cylinder when it reaches at the bottom of the plane ?
A√2gh3B√2ghC√4gh3D√3gh2The ratio of the time taken by a solid sphere and that taken by a disc of the same mass and radius to roll down a smooth inclined plane from rest from the same height -
A15:14B√15:√14C14:15D√14:√15A solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
A12R√ghB2R√ghC2R√gh3D2R√gh2
A solid cylinder rolls down an inclined plane from a height h. At any moment the ratio of rotational kinetic energy to the total kinetic energy would be
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View SolutionA cyclist wants to loop a loop inside a death globe of radius 5 m. Calculate the least velocity the cyclist should have at the lowest point and calculate the height from which he should start ?
View SolutionA body is allowed to slide down a frictionless inclined track under gravity from a height of 10 cm . The track ends in a circular loop of diameter D. The body is just able to complete the circular track , then the diameter of the track will be
View SolutionA solid sphere rolls down a smooth inclined plane of height h. If it stats from rest then the speed of the sphere when it reaches the bottom is given by
View Solution
