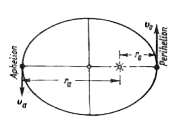
The point of an elliptical orbit closest to the Sun is called the perihelion, and the point most distant from it is called aphelion (Fig). Denoting the distance from the perihelion to the Sun by $r_{0}$ and the velocity of the planet at the perihelion by $v_{0}$ , find the radius of curvature of the orbit at the perihelion and at the aphelion, the distance from the aphelion to the Sun, and the velocity of the planet at the aphelion.
Prove that the motion of a planet in an elliptical orbit is only possible, if its total energy is negative.

Text Solution

Verified by Experts

The correct Answer is: $R_{0} = - \frac{2 r_{0} K_{0}}{U_{0}}; r_{0} = - \frac{r_{0} K_{0}}{W}; V_{a} = \frac{v_{0} W}{K_{0}}$

Denote the radius of curvature in the perihelion by $R_{0}$ the kinetic energy of the planet in perihelion by $K_{0} = m v_{0}^{2} / 2$ and its
potential energy $U_{0} = - γ m M / r_{0}$
To find the radius of curvature in the perhelion apply Newton.s second law
$\frac{m v_{0}^{2}}{R_{0}} = \frac{γ m M}{r_{0}^{2}}$ form which $R_{0} = \frac{m v_{0}^{2} r_{0}^{2}}{γ M m} = - \frac{2 r_{0} K_{0}}{U_{0}}$
The radius of curvature at the aphelion is the same as in the perihelion since the ellipse is a symmetrical figure. We have, according to Newton.s second law,
$\frac{m v_{a}^{2}}{R_{0}} = \frac{γ m M}{r_{a}^{2}}$
The total mechanical energy of the planet, according to the law of conservation of energy is
$W = \frac{m v_{0}^{2}}{2} - \frac{γ m M}{r_{0}} = \frac{m v_{a}^{2}}{2} - \frac{γ m M}{r_{a}}$
Eliminating the velocity we obtain
$\frac{γ m M R_{0}}{2 r_{0}^{2}} - \frac{γ m M}{r_{0}} = \frac{γ m M R_{0}}{2 r_{a}^{2}} - \frac{γ m M}{r_{a}}$
Cancelling out $γ m$ we obtain a quadratic equation
$r_{a}^{2} (2 r_{0} - R_{0}) - 2 r_{a} r_{0}^{2} + R_{0} r_{0}^{2} = 0$
The first root of the equation is $r_{a} = r_{0}$ This means that in this case the ellipse reduces to a circle of radius ro. In this case the radius of curvature is also $R_{0} = r_{0}$ , and, consequently, the orbital velocity is $r_{a} = \frac{r_{0} R_{0}}{2 r_{0} - R_{0}} = - \frac{r_{0} K_{0}}{W}$
Since the distance from the aphelion to the Sun is a positive quantity we must have $W < 0$ . This means that a planet can move in an elliptical orbit only if the sum of its kinetic and potential energies (i.e. its total mechanical energy) is negative. In particular in the case of a circular orbit, $W = - \frac{γ m M}{2 r_{0}}$

Updated on:21/07/2023

|

Class 12 PHYSICS NEWTONS LAW OF MOTION

Similar Questions

Knowledge Check

The earth reaches its perihelion in:
AOctober
BSeptember
CJuly
DJanuary
During the phenomenon of aphelion, the approximate distance between the earth and the sun is:
A137 million km
B147 million km
C142 million km
D152 million km
During the phenomenon of aphelion, the approximate distance between the earth and the sun is:
A137 million km
B152 million km
C147 million km
D142 million km

Recommended Questions

Home
Ask Doubt
Profile