A gas rotates in a centrifuge. Taking into account that the field of centrifugal forces of inertia is equivalent to a gravitational field, write the expression for the barometric distribution in the centrifuge.
The correct Answer is:n=n0emω2r22kT
To solve the problem one should calculate the potential energy in the field of centrifugal forces:
U=−W=−12Fl=−12 Ictt=−12mω2r2.
Substituting it into formula (26.26), we obtain the result sought.
Similar Questions
A midpoint of a thin uniform rod AB of mass m and length l is rigidly fixed to a rotation axle OO′ as shown in figure. The rod is set into rotation with a constant angular velocity ω. Find the resultant moment of the centrifugal forces of inertia relative to the point C in the reference frame fixed to the axle OO′ and to the end.
 View Solution
View SolutionCalculate the ratios of the following accelerations: the acceleration w1 due to the gravitational force on the Earth's surface, the acceleration w2 due to the centrifugal force of inertia on the Earth's equator, and the acceleration w3 caused by the Sun to the bodies on the Earth.
View Solution
Knowledge Check
- Question 1 - Select One
Motion of a spinning ‘top’ is an example of
A. Centripetal Force
B. Centrifugal Force
C. Gravitational Force
D. Frictional ForceACBBCADD - Question 2 - Select One
Motion of a spinning ‘top’ is an example of
A. Centripetal Force
B. Centrifugal Force
C. Gravitational Force
D. Frictional ForceACBBCADD - Question 3 - Select One
Assertion: If a particle is rotating in a circle, then centrifugal force is acting on the particle in radially outward direction .
Reason: centrifugal force is equal and opposite to the centripetal force.AIf both Assertion and Reason are correct and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.CIf Assertion is true but Reason is false.DIf Assertion is false but Reason is true.
Centrifuging may be used for the separation of isotopes. To do this a mixture of two gases is placed inside a cylindrical vessel rotating at a high speed. Because of the action of centrifugal forces, the isotope concentration near the cylinder wall will be different from that in the contre.
Compare the concentrations of the light and the heavy uranium isotopes near the centrifuge walls, if the diameter of the cylinder is 10 cm, the rotation speed is 2.0×103 r. p.s., the temperature of uranium hexafluoride is 27∘C. For concentrations in normal conditions see ξ25.6.
Find the enrichment factor in the mixture of the heavy isotope near the walls of the vessel. The term enrichment factor applies to the quotient obtained by dividing the concentration ratio during rotation by the initial concentration ratio:
x=(n2n1)(n02n01)View SolutionA small body of mass m=0.30kg starts sliding down from the top of a smooth sphere of radius R=1.00m. The sphere rotates with a constant angular velocity ω=6.0rad/s about a vertical axis passing through its centre. Find the centrifugal force of inertia and the Coriolis force at the moment when the body breaks off the surface of the sphere in the reference frame fixed to the sphere.
View SolutionAssertion If a particle is rotating in a circle, then centrifugal force is acting on the particle in radially outward direction .
Reason centrifugal force is equal and opposite to the centripetel force.View SolutionDemonstrate that in the reference frame rotating with a constant angular velocity ω about a stationary axis a body of mass m experiences the resultant
(a) centrifugal force of inertia Fcf=mω2RC, where RC is the radius vector of the body's centre of inertia relative to the rotation axis,
(b) Coriolis force Fcor=2m[v′Cω], where v′C is the velocity of the body's centre of inertia in the rotating reference frame.View SolutionA centrifuge has a horizontal cylinder rotating about a vetical axis as shown in the figure. Water inside it has density ρ.
(a) Consider a point A. Inside the liquid, at a distance r from the rotation axis. Liquid pressurea t his point is P. Write the value of dPdr when the cylinder, with all its liquid. rotates uniformly at an angular speed ω.
(ii) Consider a small disc shaped foreign material inside the centrifuge at point A. The area of circular disc is ΔS and its thickness is Δr. It disc is in position so that its circular face is vertical. Find the radial acceleration of the disc with respect to the cylinder when angular speed of rotation is
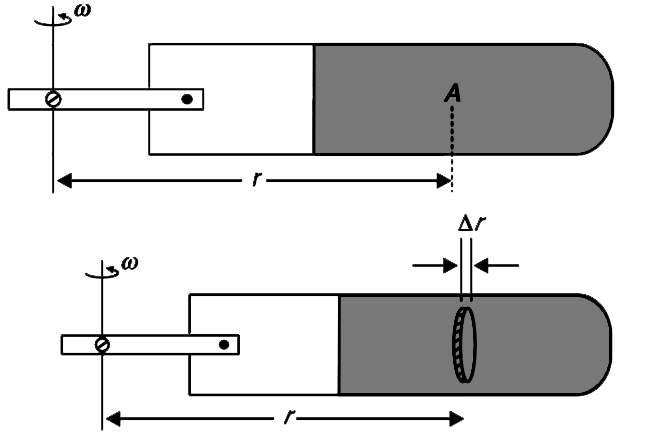 View Solution
View Solution

