Derive the Bernoulli equation for an incompressible liquid flowing in an inclined tube of variable cross section in a gravitational field.
The correct Answer is:Hint . Note that in this case the work done by the forces of pressure is equal to the change in the total mechanical energy (p+ρv22+ρgh=const)
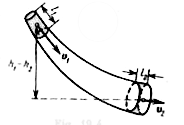
Apply the law of conservatiou of energy in conservative systems. In our case the work of the forces of pressure is accompaniod by the change in the total mechanical energy of the system : W=W2−W1=(K2+U2)−(K1+U1). Consider separately a volume of liquid V=l1S1=l2S2 (Fig.), the mass of the this volume is m=ρV. The work of the forces of pressure is
W=F1l1−F2l2=p1S1l1−p2S2l2=(p2−p1)V
Subtituting the result obtained into the expression for the change in energy , we obtain
(p1−p2)V=mv222+mgh2−mv212−mgh1
whence
p1+ρv212+ρgh1=p2=ρv222+ρgh2
Similar Questions
Using the Bernoulli equation for a compressible flow derive the relation between the velocity of the flow at a given point and the local sound velocity.
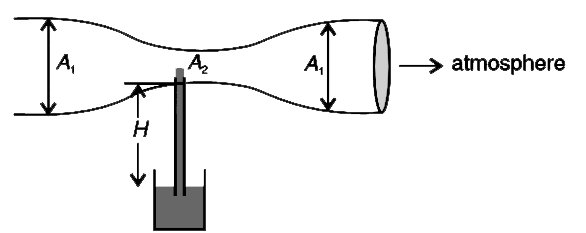
View Solution(i) Air (density=ρ) flows through a horizontal venturi tube that discharges to the atmosphere. The area of cross section of the tube is A1 and at the constriction it is A2. The constriction is connected to a water (density=ρ0) tank through a vertical pipe of lenght H. Find the volume flow rate (Q) of the air through tube that is needed to just draw the water into the tube.
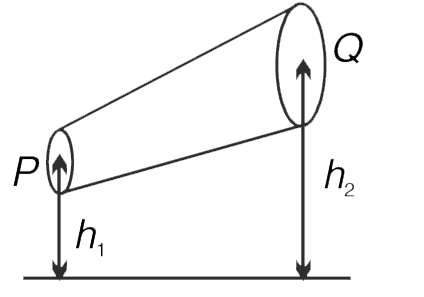
(ii) A non viscous liquid of constant density ρ flows in a stremline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in the figure. The area of cross section of the tube at two points P and Q at heights of h1 and h2 are respectively A1 and A2. The velocity of the liquid at point P is v. Find the work done on a small volume ΔV of fluid by the neighbouring fluid as the small volume moves from P to Q.
View Solution
Knowledge Check
An incompressible liquid flows through a horizontal tube as shown in the figure. Then the velocity 'v' of the fluid is:
 A3.0 m/sB1.5 m/sC1.0 m/sD2.25 m/s
A3.0 m/sB1.5 m/sC1.0 m/sD2.25 m/sA liquid flows through a horizontal tube of variable diameter. Then the pressure is lowest where
Avelocity is lowestBvelocity is highestCdiameter is largestDboth velocity and diameter are largest
An incompressible liquid flows through a horizontal tube as shown in the figure. Then the velocity 'v' of the fluid is:

View SolutionA non-viscous liquid of constant density 1000kg/m3 flows in a streamline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in Figure. The area of cross section of the tube two point P and Q at heights of 2 metres and 5 metres are respectively 4×10−3m2 and 8×10−3m2. The velocity of the liquid at point P is 1m/s. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q.
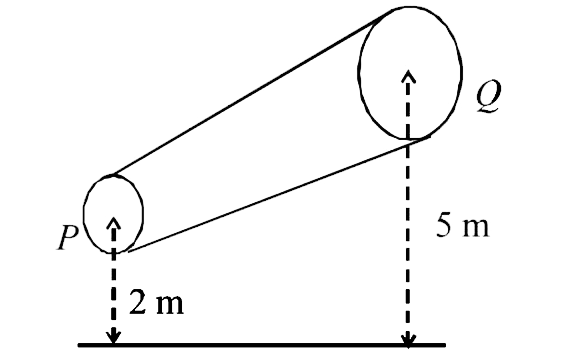
View SolutionA non-viscous liquid of constant density 1000kg/m3 flows in a streamline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in Figure. The area of cross section of the tube two point P and Q at heights of 2 metres and 5 metres are respectively 4×10−3m2 and 8×10−3m2. The velocity of the liquid at point P is 1m/s. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q.

View SolutionA: Bernoulli's theorem holds good only for non viscous and incompressible liquid.
R: Bernoulli’s theorem is based on the conservation of energy
View SolutionBernoulli's equation is derived on the basis of _______.
View SolutionWhich of the following equation is correct in the context of kohlarusch 's law
View Solution
