Imagine an infinitely long one-dimensional ionic erystal-a chain of alternating positive and negative ions with a distance a between them (Fig.). Find the force with which one half of the chain acts on an arbitrary ion and compare the result with the force to acting between the two adjacent ions. Calculation accuracy should be better than 0.001.
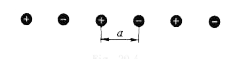
The correct Answer is:F=0.82F0
The force sought is of the form
F=−e24πε0a2(1−122+132−142+…)=
=−e24πε0a2(312.2^2+732.4^2+1152.6^2+..)
Compute the value of the series in the brackets to three significant digits. To obtain the required accuracy, we may discard all terms below 0.001, i.e. we may take the sum of the first ten terms in the series. We obtain
312.2^2+732.4^2+....+39192.20^2 =
=0.82128≈0.82
Hence F=−0.82e24πε0a2
This means that neglecting the interactions with all the ions except the nearest neighbours results in an error of no greater than 20% .
Similar Questions
In a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was 103ms−1and2×103ms−1 for first and second particle, respectively, and mass of these particles were 2×10−30kgand10−30kg, respectively. Distance between them were 12Å(1Å = 10^(-10)m).
Paths of the two particles was
View SolutionIn a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was 103ms−1and2×103ms−1 for first and second particle, respectively, and mass of these particles were 2×10−30kgand10−30kg, respectively. Distance between them were 12Å(1Å = 10^(-10)m).
Acceleration of the first particle was
View Solution
Knowledge Check
In a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was 103ms−1and2×103ms−1 for first and second particle, respectively, and mass of these particles were 2×10−30kgand10−30kg, respectively. Distance between them were 12Å(1Å = 10^(-10)m).
Paths of the two particles wasAintersecting straight linesBparabolicCcircularDstraight line with respectIn a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was 103ms−1and2×103ms−1 for first and second particle, respectively, and mass of these particles were 2×10−30kgand10−30kg, respectively. Distance between them were 12Å(1Å = 10^(-10)m).
if the first particle is stopped for a moment and then released, the velocity of center of mass of the system just after the release will beA13×10−30ms−1B13×103ms−1C23×103ms−1Dnone of theseIn a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was 103ms−1and2×103ms−1 for first and second particle, respectively, and mass of these particles were 2×10−30kgand10−30kg, respectively. Distance between them were 12Å(1Å = 10^(-10)m).
Acceleration of the first particle wasAzeroB4×1016ms−2C2×1016ms−2D2.5×1015ms−2
In a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was 103ms−1and2×103ms−1 for first and second particle, respectively, and mass of these particles were 2×10−30kgand10−30kg, respectively. Distance between them were 12Å(1Å = 10^(-10)m).
if the first particle is stopped for a moment and then released, the velocity of center of mass of the system just after the release will be
View SolutionIn a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was 103ms−1and2×103ms−1 for first and second particle, respectively, and mass of these particles were 2×10−30kgand10−30kg, respectively. Distance between them were 12Å(1Å = 10^(-10)m).
Acceleration of the second particle was
View Solution(a) Two protons are placed at some separation in vacuum. Find the ratio of electric and gravitational force acting between them.
(b) Two point charges are placed at separation 3m in vacuum. What can be the minimum force between them.
(c ) A charge Q is to be divided on two objects. What should be the value of the charges in the objects so that the force between them is maximum ?
(d) Two insulating small spheres are rubbed against each other and placed 1.6cm apart. If they attract each other with a force of 0.9N, how many electrons were transferred from one sphere to the other during rubbing ?
View SolutionIn a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was 103ms−1and2×103ms−1 for first and second particle, respectively, and mass of these particles were 2×10−30kgand10−30kg, respectively. Distance between them were 12Å(1Å = 10^(-10)m).
Acceleration of the second particle was
View SolutionPassage 1
The second section gives power to the President, "by and with the advice and consent of the Senate, to make treaties, provided two thirds of the Senators present concur…"
Some are displleased with it, not on account of any errors or defects in it, but because they say the treaties will have the force of laws, and thus should be made only by the legislature. These gentlemen seem not to consider that the judgement of our courts, and the commissions constitutionally given by our governor, are as valid and as binding on all persons whom they concern as the laws passed by our legislature. All constitutional acts of power, whether in the executive or in the judicial department, have as much legal validity and obligation as if they proceeded from the legislature. it surely does not follow that because the people have given the power of makin laws to the legislature, they should therefore likewise give the legislature the power to do every other act of government by which the citizens are to the bound and affected. The President is to have power, "by and with the advice and consent of the Senate, to make treaties, provided two thirds of the senators present concur."...
Though several writers o teh subject of government place the power of making treatis in the class of executive aunthorities, this is evidently an arbitrary classicication, for if we attend carefully to its operation, it will be found to partake more of the legislative than of the executive character, though it does not seem strictly to fall within the definition of either of them. The essence of teh legislative branch is to enact laws, or, in other words, to prescribe rules for the regulation of teh society, while the execution of the laws, and the employment of the common strength, either for this purpose of for the common defense, seem to comprise all the functions of the executive branch. The power of making treaties is, plainly, neither the one nor the other. It relates neither to the execution of the existing laws, nor to the creation of new ones, and still less to an exertion of the common strength. Its objects are CONTRACTS with foreign nations, which have the force of law, but derive it from the obligations of good faith. They are not rules prescribed by the government of the citizen, but agreements between two governments. The power in questin seems therefore to form a distinct department, and to belong, properly, neither to the legislative nor to the exective branch. The qualties elsewhere detailed as indispensable in the management of foreign negotiations point to the Exective as the best agent in those transactions, while the vast importance of the trust, and the operation of treaties as laws, plead strongly for the participation of the whole or a portion of the legislative body in the office of making them.
Which choice best states the relationship between the two passages ?
View Solution
