A copper rod is fixed between two supports. Its temperature was raised

A rod of aluminium is fixed between two rigid support. If the temperature of rod is increased by $10 ° C$ , then the thermal stress on the rod is (Take Y= $7 \times 10^{10}$ Pa and $α$ =2.4* $10^{- 5} K^{- 1}$ )
A $1.4 \times 10^{3}$ Pa
B $1.7 \times 10^{7}$ Pa
C $1.7 \times 10^{3}$ Pa
D $2.4 \times 10^{7}$ Pa
A unifrom rod is fixed at one end to a rigid support, its temperture is gradually increased the representaion of graph strain $(e)$ versus increment in temperature $Δ θ$ is

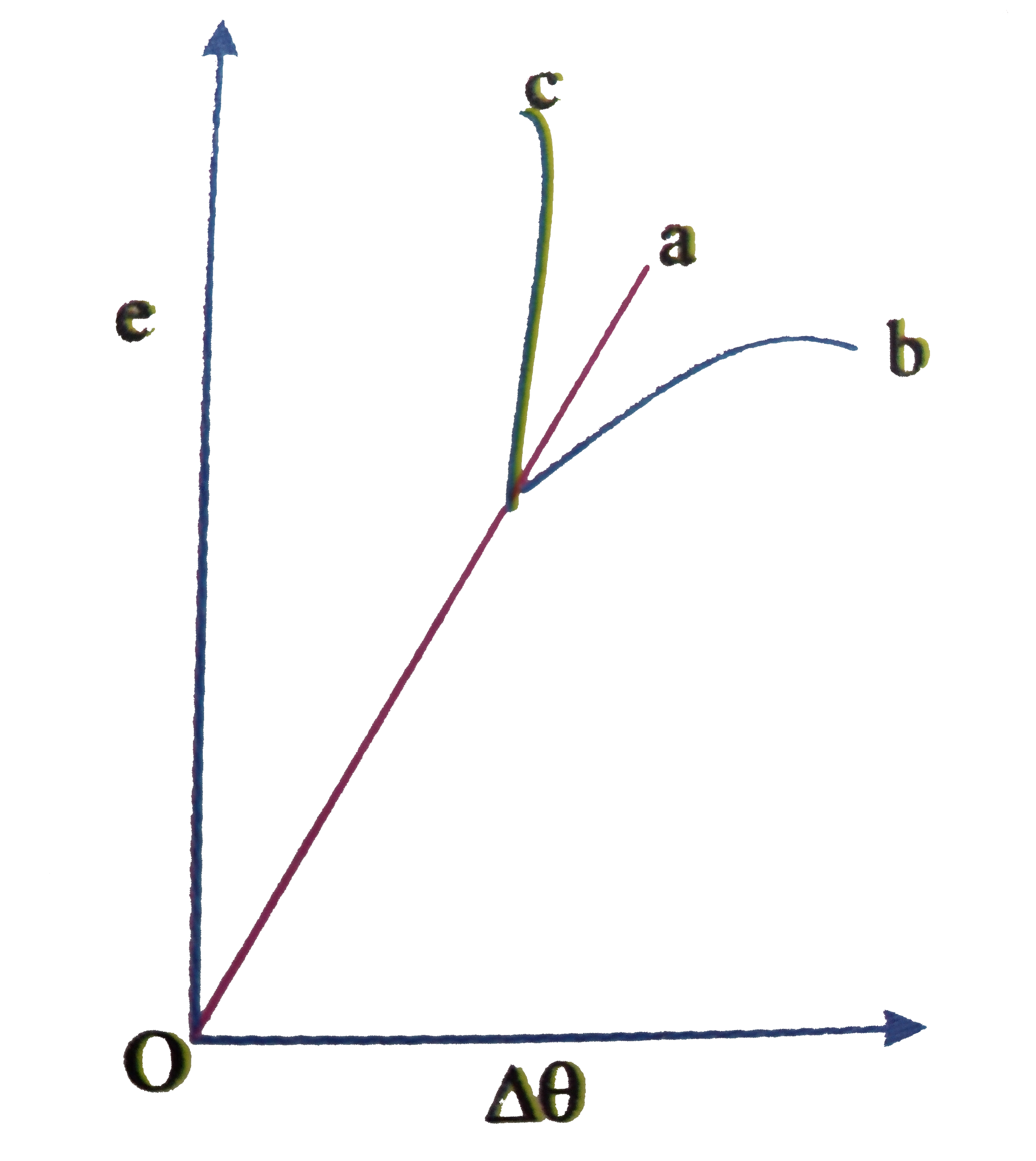A $d$
B $a$
C $C$
D $b$
A metal rod of Young's modules Y and coefficient of thermal expansion $α$ is held at its two ends such that its length remains constant. If its temperature is raised by $t^{\circ} C$ , the linear stress developed in it is
A $Y α t$
B $\frac{1}{Y α t}$
C $\frac{α t}{Y}$
D $\frac{Y}{α t}$

A copper rod is fixed between two supports. Its temperature was raised by $50^{\circ} C$ . What is the resulting stress in the rod?