A dipole is placed in the field of a point charge, the distance between the dipole and the field source being much greater than the dipole separation. Find the force acting on the dipole and the torque, if the dipole is arranged:
In the direction of the line of force.
It is evident from Fig. 24.8b that in this case two forces act on the dipole in the direction of the radius vector. Hence it is clear that in the latter case the torque is zero, and the resultant acts in the direction of the radius to the source. The resultant can be found by two methods.
One may use the Coulomb law:
F=F−+F+=−Qq4πε0(r−l/2)2+Qq4πε0(r+l/2)2
=−2Qrql4πε0(r2−l2/4)2
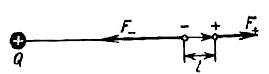
Noting that the problem stipulates that l<<r, we obtain
F=02Qrql4πε0r4=−2Qp04πε0r3
The same result may be obtained from formula (37.15), if the derivative is substituted for the ratio of increments. We have
F=pe=dEdr=Peddr(Q4πε0r2)=−2Qpe4πε0r3
Similar Questions
A dipolo is placed in the field of a point charge, the distance between the dipole and the field source being much greater than the dipole separation. Find the force acting on the dipole and the torque, if the dipole is arranged:
perpendicular to the line of force.
View SolutionA dipolo is placed in the field of a point charge, the distance between the dipole and the field source being much greater than the dipole separation. Find the force acting on the dipole and the torque, if the dipole is arranged:
perpendicular to the line of force.
View Solution
Knowledge Check
An electric dipole in a uniform electric field has potential energy U. The magnitude of the torque acting on the dipole due to the field is τ.
AU is minimum and τ is zero when the dipole is perpendicular to the field.BU is zero and τ is a maximum when the dipole is perpendicular to the field.CU is a minimum and τ is a maximum when the dipole is perpendicular to the field.DU is a minimum and τ is zero when the dipole is anti-parallel to the field.(i) State Maxwell's right-hand thumb rule.
(ii) PQ is a current carrying conductor in the plane of the paper as shown in the figure. Mention the direction of magnetic fields produced by it at points A and B. Given r1<r2, where will the strength of the magnetic field be larger?
Justify your answer in each case.
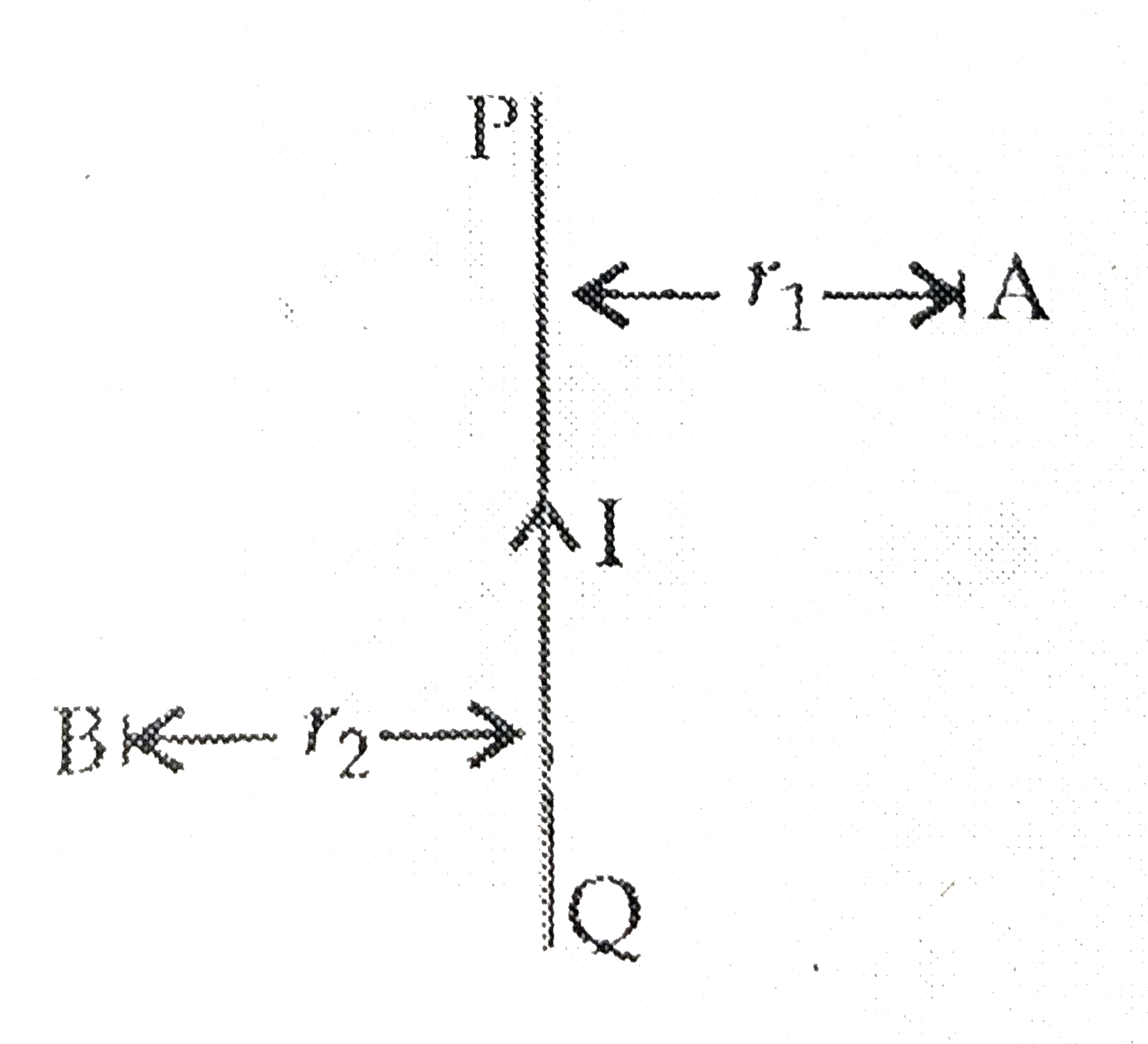 APEBPE sin θCPE cos θD0
APEBPE sin θCPE cos θD0A dipole of moment →p is placed in a uniform electric field →E. The force on the dipole is →F and the torque is →τ
A→F=0B→F=|→p|→EC|→τ|=→p.→ED→τ=→p×→E
A short electric dipole is placed in the electric field due to a point charge. Then (A) The dipole must experience a force (B) The dipole may experience a force (C) The dipole must experience a torque (D) The dipole may experience a torque
View SolutionA point-like charge Q and a dipole with an electric moment Pel are separated by a distance that is considerably larger than the arm of the dipole, with the result that the dipole may be considered as being point. The dipole's axis lies :'along the lines of force 'of the point charge. Compare the force acting on the di pole ill the field of the point charge with t.hat acting on the point charge ill the Held of the di pole.
View SolutionForce and torque on a dipole|| potential energy OF dipole
View SolutionAn electric dipole is placed in a uniform electric field. The net electric force on the dipole
View SolutionA dipole of moment →p is placed in a uniform electric field →E. The force on the dipole is →F and the torque is →τ
View Solution
