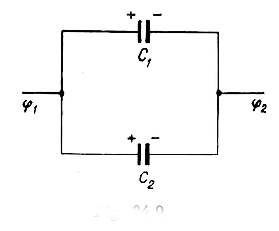
Two capacitors with capacitances C1andC2 are connected in parallel. Find the resultant capacitance.
When the capacitors are connected in parallel (Fig. 24.9), all their interconnected plates have the same potential, therefore q1=C1(φ1−φ2)andq2=C2(φ1−φ2), where q1andq2 are the charges of the respective capacitors. The charge of the system is
q=q1+q2=(C1+C2)(φ1−φ2).
On the other h and q=C(φ1−φ2), where C is the equivalent capacitance. Hence the formula sought.
Similar Questions
Two capacitors with capacitances C1andC2 are connected in series. Find the resultant capacitance.
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View Solution
Knowledge Check
Two capacitors of capacitances C1andC2 are connected in parallel. If a charge q is given to the assembly, the charge gets shared. The ratio of the charge on the capacitor C1 to the charge on C2 is
AC1C2BC2C1CC1C2D1C1C2Two capacitors of capacitances C1 and C2 are connected in parallel. If a charge Q is given to the combination, the ratio of the charge on the capacitor C1 to the charge on C2 will be
AC1C2B√C1C2C√C2C1DC2C1The equivalent capacitance of three capacitors of capacitance C1:C2 and C3 are connected in parallel is 12 units and product C1.C2.C3=48. When the capacitors C1 and C2 are connected in parallel, the equivalent capacitance is 6 units. then the capacitance are
A2,3,7B1.5,2.5,8C1,5,6D4,2,6
Two capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionThe same capacitors are connected in series. Find the resultant capacitance.
View SolutionTheee capacitors of capacitance 1,2,and 3 μF connected in series. Find the resultant capacitance.
View SolutionTwo capacitors of capacitance C1=2μF and C2=8μF are connected in series and the resulting combination is connected across 300 volts. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionThe equivalent capacitance of three capacitors of capacitance C1:C2 and C3 are connected in parallel is 12 units and product C1.C2.C3=48. When the capacitors C1 and C2 are connected in parallel, the equivalent capacitance is 6 units. then the capacitance are
View Solution
