Several identical capacitors were connected in parallel and charged to a voltage φ0. Subsequently they were reconnected in series with the aid of a switch. What will be the voltage across the terminals? Will the energy of the system change?
The solution is obvious from Figs. 24.11a and 24.11b, which give the diagrams of the parallel and series connections of four identical capacitors. The energy in the case of parallel connection is
Wpar=CparΨ2par2=nCnφ202
and of series connections
Wser=Cserφ2ser2=(C0/n)n2φ202=Wpar
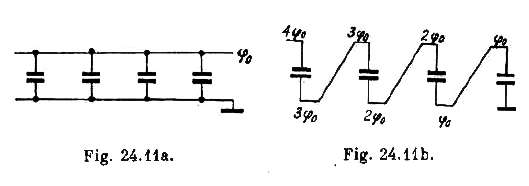
Similar Questions
N identical capacitors are connected in parallel which are charged to a potential V. If these are separated and connected in series then what potential difference will be obtained?
View SolutionTwo identical planar capacitor connected in parallel and charged to a voltage U0=12V. When you disconnect them from the voltage source, the distance between the plates of one of the capacitors is reduced to one third of the original distance. What will be the new voltage on the capacitors ?
View Solution
Knowledge Check
Two identical capacitors are connected in series with a source of constant voltage V. If Q is the charge on one of the capacitors, the capacitance of each capacitor is :
AQ/2VBQ/VC2Q/VDNone of theseA diode is connected to 220V(rms) ac in series with a capacitor as shown in fig. The voltage across the capacitor is
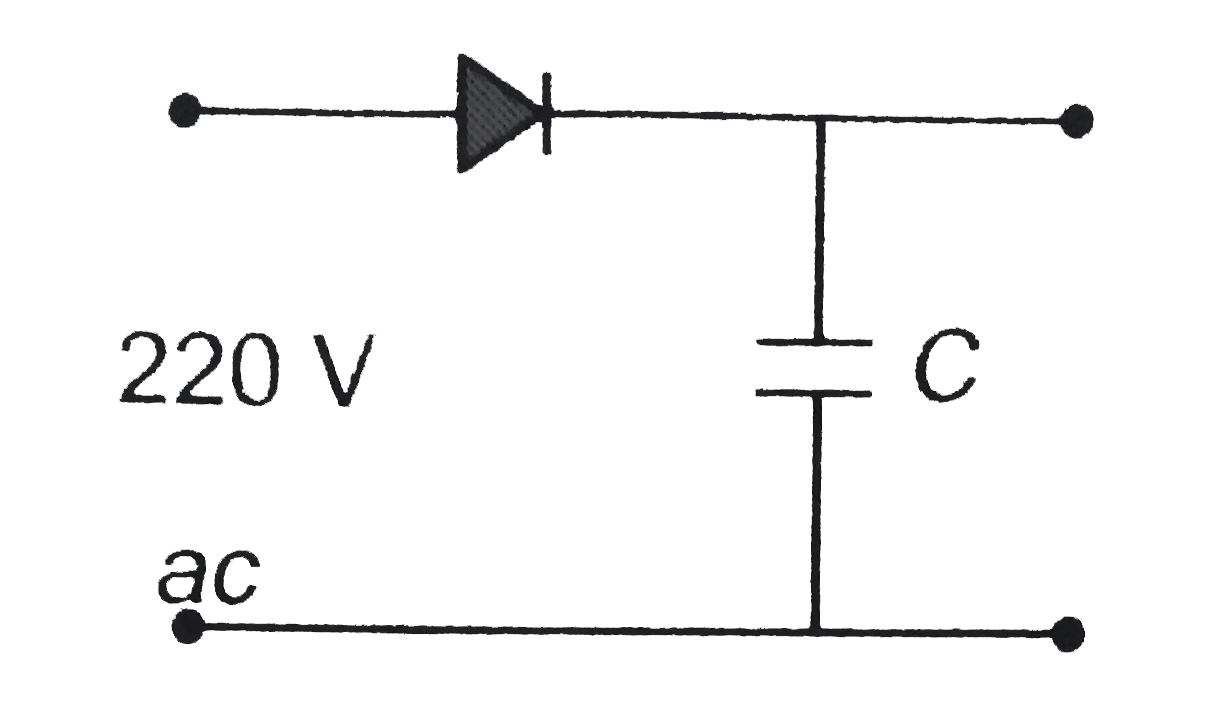 A220VB110VC311.1VD220√2V
A220VB110VC311.1VD220√2Vn identical capacitors are connected in parallel to a potential difference V. These capacitors are then reconnected in sereis, their charges being left undisturbed. The potential difference obtained is
AzeroB(n−1)VCnVDn2V
n identical capacitors are connected in parallel to a potential difference V. These capacitors are then reconnected in series, their charges being left undisturbed. The potential difference obtained is
View SolutionTwo capacitors 2μFand4μF are connected in parallel. A third capacitor of 6μF capacity is connected in series. The combination is connected across a 12 V battery. The voltage across a 2μF capacitor is

View SolutionTwo capacitors of capacities 1μF and 4μF are connected in series with battery of 200V. The voltage across them are in the ratio of
View SolutionTwo capacitors 2μF and 4μF are connected in parallel. A third capacitor of 6μFis connected in series. The combination is then connected across a 12V battery. The voltage across 2μF capacitor is:
View SolutionTwo capacitors 2μFand4μF are connected in parallel. A third capacitor of 6μF capacity is connected in series. The combination is connected across a 12 V battery. The voltage across a 2μF capacitor is

View Solution
