Determine the load resistance for which the power delivered to the circuit is a maximum. Graph the dependence of the power on the load resistance.
The power Rtot=ε2/(R+r) is at its maximum in conditions of short-circuit (R =0). The short circuit power is Rsh.e=ε2/r.
The power in the external circuil is at its maximum when R = r.
To check this consider the extremum of the expression Pex=ε2r.Rr(R+r)2=ε2ry
We have
y=(R+r)2Rr=Rr+2+rR=Rr−2+rR+r=
=(√Rr−√rR)2+4
Obviously, y= 4 for R = r is minimum value. In this case the power in the external circuit is maximum. The corresponding graphs are shown in Fig. 26.13. 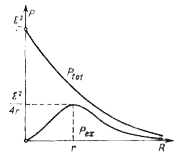
Similar Questions
Knowledge Check
Power delivered by the source of the circuit becomes maximum , when :
AωL=ωCBωL=1ωCCωL=−(1ωC)2DωL=√ωCIn the circuit Fig., what is the range over which the load resistance can be varied?
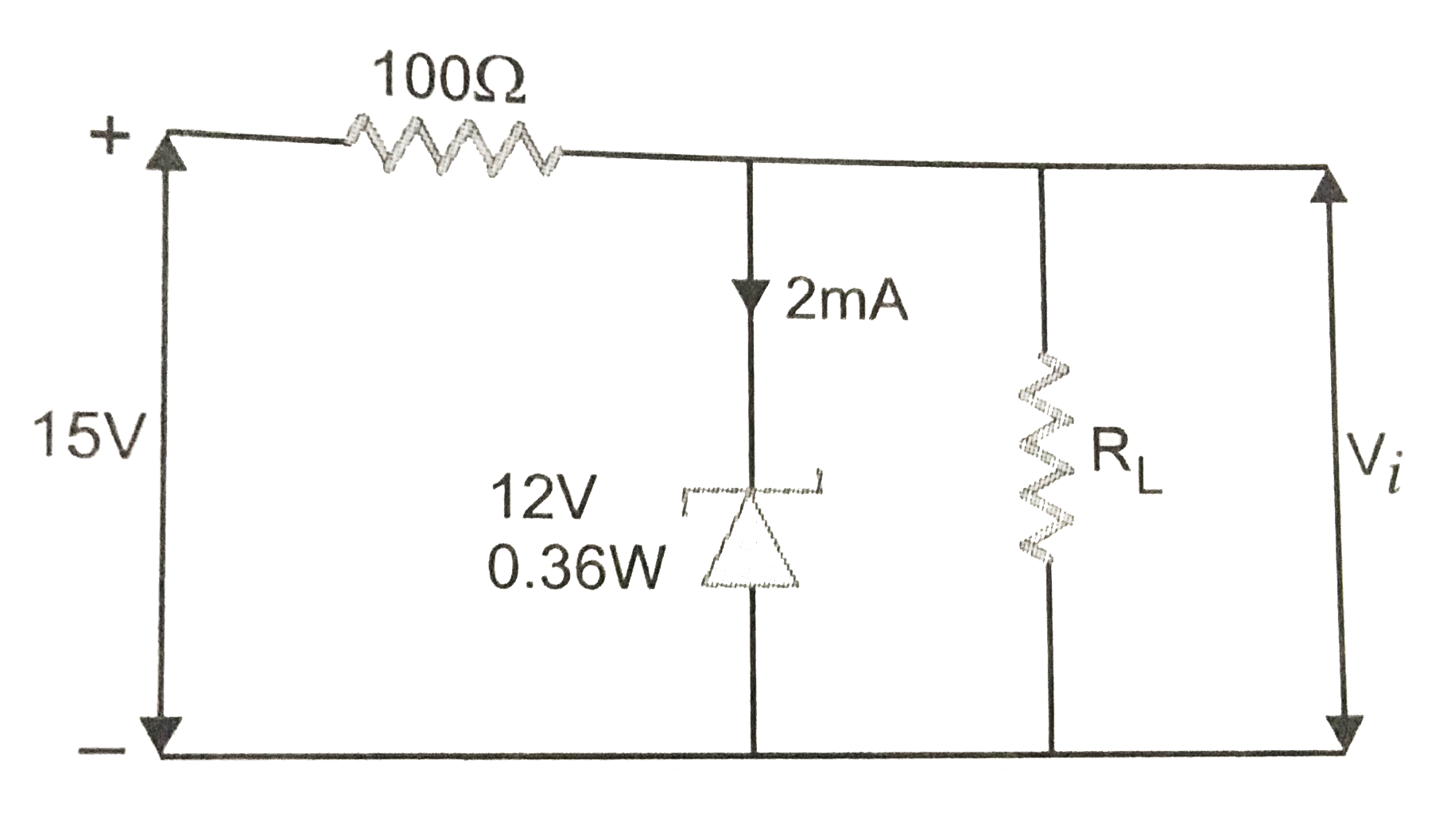 A298.6Ω≤RL<∞B303.7mega≤RL<∞ onlyC408.2mega≤RL<∞ onlyD428.6mega≤RL<∞ only
A298.6Ω≤RL<∞B303.7mega≤RL<∞ onlyC408.2mega≤RL<∞ onlyD428.6mega≤RL<∞ only
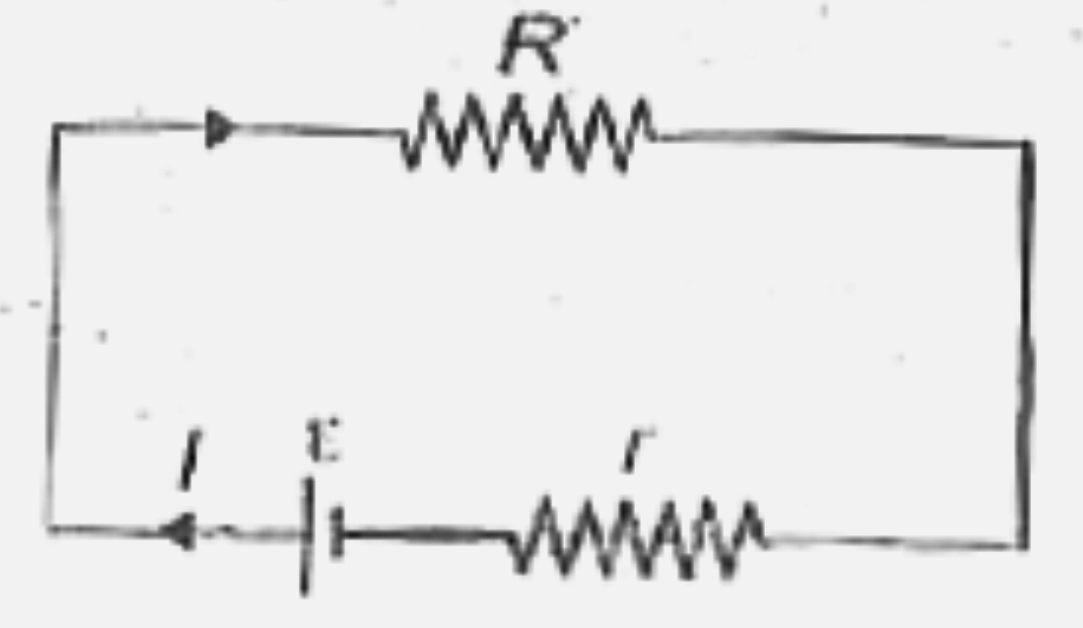
A cell of emf ε and internal resistance r is connected across a load resistance R .
(i) Find the maximum power delivered at the load ?
(ii) Draw the power (P) vs load resistance (R) graph .
View SolutionA battery of emf ε and internal resistance r is connected across a pure resistance device (e.f. and electric heater or an electric bulb) of resistance R. Show that the power output of the device is maximum when there is a perfect 'mathcing' between the external resistance adn the source resistance (i.e., where R=r). Determine the maximum power outpur.
Or
State and prove the maximum power theorem. show that the effciency of a battery when delivering maximum power is only 50%
(b) What is power output of the source abvoe if the battery is hosrted? what is the power dissipation inside the battery in that case?
View SolutionA battery of emf ε and internal resistance r is connected across a pure resistance device (e.f. and electric heater or an electric bulb) of resistance R. Show that the power output of the device is maximum when there is a perfect 'mathcing' between the external resistance adn the source resistance (i.e., where R=r). Determine the maximum power outpur.
Or
State and prove the maximum power theorem. show that the effciency of a battery when delivering maximum power is only 50%
(b) What is power output of the source abvoe if the battery is hosrted? what is the power dissipation inside the battery in that case?
View SolutionA power supply with an e.m.f ε and internal resustance r is connected to a variable resistance R. Find the dependence of the total power generated by the supply and of the power delivered to the external circuit on the load resistance.
View SolutionA power supply with an e.m.f ε and internal resustance r is connected to a variable resistance R. Find the dependence of the total power generated by the supply and of the power delivered to the external circuit on the load resistance.
View SolutionIf a load resistance r then power supplied by the cell to load R is maximum if ….. And maximum power is given by …..
View Solution
