In modern diodes the anode is often brought very close to the cathode so Dial their areas are approximately equal. Assuming the electrons to leave the cathode with zero velocity find the force with which they act on the anode. The current in the tube is isat=500mA, the anonded voltage is φa=600V.
The correct Answer is:4.1×10−5 N.
The collision of the electrons with the anode is an inelastic one, and this makes it possible to compute the force using formula (17,19) form ∮17.5 Noting that the current is
F=imve=ie√2eφm
Similar Questions
Figure 33.5 depicts the grid characteristics of a triode plotted at anode voltages of 450 V and 600 V. Find the triode's internal resistance Ri in the linear section of the characteristic and its amplification factor μ, i.e. the ration of the change in the anonde voltage to the change in the grid voltage which cauases a given change in the anode current.
View SolutionFigure 33.5 depicts the grid characteristics of a triode plotted at anode voltages of 450 V and 600 V. Find the triode's internal resistance Ri in the linear section of the characteristic and its amplification factor μ, i.e. the ration of the change in the anonde voltage to the change in the grid voltage which cauases a given change in the anode current.
View Solution
Knowledge Check
The basic principle underlying the hall effect is the Lorentz force. Whenk an electron moves along a direction perpendicular to an applied magnetic field. It exeriences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an - n-type bar shaped semiconductor, the carries are predominatly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward the negative z-axis resulting in an excess surface electrical charge on the sides of the sample. this charge results in the hall voltage a potential drop across the two sides of the sample
Thre transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnD, where I is the current B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure (z1=11.8mm and = 0.23 mm) carrying a current of 120 A in the x -direction in unifrom magnetic field B = 0.95 T. If electron density is 5.85×1028/m3 then
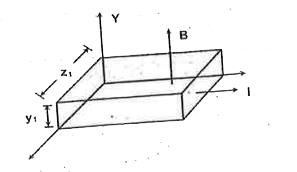
magnitude of the drift velocity of electron isA2.35 mm/sB4.7 mm/sC7.5 mm/sD9.4 mm/s
Answer question on the basis of your understanding of the following paragraph and the related studied concepts :
Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current.
When an external electric field →E is applied across a piece of conductor, electrons will be accelerated at →a=e→Em . If →a was the velocity of electron after the last collision then velocity →vt after a time t will be →vt=→u+→at
The average velocity of the electrons at time t is the average of all→v' s. However, average value of →u's is zero. As collisions of the electrons occur at random times, let τ be the average time between successive collision and then the average velocity electrons is expressed as →vd (known as the drift velocity) and is given as:
→vd=−e→Emτ
This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : I=nAevd, where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of 10−3ms−1 for currents in the range of a few amperes.
If the electron drift speed is so small and the electron charge is small, how can we still obtain large amounts of current even in a thin conducting wire ?
View SolutionAnswer question on the basis of your understanding of the following paragraph and the related studied concepts :
Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current.
When an external electric field →E is applied across a piece of conductor, electrons will be accelerated at →a=e→Em . If →a was the velocity of electron after the last collision then velocity →vt after a time t will be →vt=→u+→at
The average velocity of the electrons at time t is the average of all→v' s. However, average value of →u's is zero. As collisions of the electrons occur at random times, let τ be the average time between successive collision and then the average velocity electrons is expressed as →vd (known as the drift velocity) and is given as:
→vd=−e→Emτ
This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : I=nAevd, where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of 10−3ms−1 for currents in the range of a few amperes.
Are the paths of electrons straight lines between successive collisions in the (i) absence of electric field, (ii) presence of electric field ?
View SolutionAnswer question on the basis of your understanding of the following paragraph and the related studied concepts :
Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current.
When an external electric field →E is applied across a piece of conductor, electrons will be accelerated at →a=e→Em . If →a was the velocity of electron after the last collision then velocity →vt after a time t will be →vt=→u+→at
The average velocity of the electrons at time t is the average of all→v' s. However, average value of →u's is zero. As collisions of the electrons occur at random times, let τ be the average time between successive collision and then the average velocity electrons is expressed as →vd (known as the drift velocity) and is given as:
→vd=−e→Emτ
This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : I=nAevd, where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of 10−3ms−1 for currents in the range of a few amperes.
Define drift velocity. On what factors does it depend ?
View SolutionAnswer question on the basis of your understanding of the following paragraph and the related studied concepts :
Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current.
When an external electric field →E is applied across a piece of conductor, electrons will be accelerated at →a=e→Em . If →a was the velocity of electron after the last collision then velocity →vt after a time t will be →vt=→u+→at
The average velocity of the electrons at time t is the average of all→v' s. However, average value of →u's is zero. As collisions of the electrons occur at random times, let τ be the average time between successive collision and then the average velocity electrons is expressed as →vd (known as the drift velocity) and is given as:
→vd=−e→Emτ
This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : I=nAevd, where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of 10−3ms−1 for currents in the range of a few amperes.
Guess the order of magnitude of thermal speed of free electrons in a conductor in the absence of an external electric field.
View SolutionAnswer question on the basis of your understanding of the following paragraph and the related studied concepts :
Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current.
When an external electric field →E is applied across a piece of conductor, electrons will be accelerated at →a=e→Em . If →a was the velocity of electron after the last collision then velocity →vt after a time t will be →vt=→u+→at
The average velocity of the electrons at time t is the average of all→v' s. However, average value of →u's is zero. As collisions of the electrons occur at random times, let τ be the average time between successive collision and then the average velocity electrons is expressed as →vd (known as the drift velocity) and is given as:
→vd=−e→Emτ
This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : I=nAevd, where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of 10−3ms−1 for currents in the range of a few amperes.
What is the rate of flow of electric field through the conductor ?
View SolutionA current i, indicated by the crosses in figure, is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angle to the strip.
(a) Calculate the drift velocity vd of the electrons.
(b) What are the magnitude and direction of the magnetic force F acting on the electrons?
(c) What should the magnitude and direction of a homogeneous electric field E be in order to counterbalance the effect of mangetic field?
(d) Calculate voltage V necessary between two sides of the conductor in order to creat this field E Between which sides of the conductor would this voltage have to be applied?
(e) If no electric field is applied from the outside, the electrons will be pushed somewhat to one side and therefore will give rise to a uniform electric field EH across the conductor until the forces of this electrostatic field EH balance the magnetic forces encountered in part (b). What will be the magnitude and direction of field EH?
Assume that n, the number of conductor electrons per unit volume is 1.1×1029m−3,h=0.02m,w=0.1cm,i=50A,andB=2T.

View SolutionA current i, indicated by the crosses in figure, is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angle to the strip.
(a) Calculate the drift velocity vd of the electrons.
(b) What are the magnitude and direction of the magnetic force F acting on the electrons?
(c) What should the magnitude and direction of a homogeneous electric field E be in order to counterbalance the effect of mangetic field?
(d) Calculate voltage V necessary between two sides of the conductor in order to creat this field E Between which sides of the conductor would this voltage have to be applied?
(e) If no electric field is applied from the outside, the electrons will be pushed somewhat to one side and therefore will give rise to a uniform electric field EH across the conductor until the forces of this electrostatic field EH balance the magnetic forces encountered in part (b). What will be the magnitude and direction of field EH?
Assume that n, the number of conductor electrons per unit volume is 1.1×1029m−3,h=0.02m,w=0.1cm,i=50A,andB=2T.

View Solution
