Find the resulting amplitude and phase of the vibrations
$s = A cos ω t + \frac{A}{2} cos (ω t + \frac{π}{2}) + \frac{A}{4} cos (ω t + π) + \frac{A}{8} cos (ω t + \frac{3 π}{2})$

Text Solution

Verified by Experts

The correct Answer is: $B = \frac{3 A \sqrt{5}}{8} = 0.84 A; φ = a r c tan \frac{1}{2} = 0.464 rad = {26.6}^{\circ}$

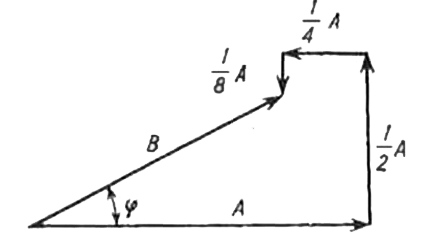
Apply the vector diagram Fig. Here
$B = \sqrt{{(A - \frac{A}{4})}^{2} + {(\frac{A}{1} - \frac{A}{8})}^{2}}, tan φ = \frac{(A / 4) - (A / 8)}{A - (A / 4)} = \frac{1}{2}$

Updated on:21/07/2023

|

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Similar Questions

Knowledge Check

For simple harmonic vibrations
$y_{1} = 8 cos ω t$
$y_{2} = 4 cos (ω t + \frac{π}{2})$
$y_{3} = 2 cos (ω t + π)$
$y_{4} = cos (ω t + \frac{3 π}{2})$ are superimposed on one another. The resulting amplitude and phase are respectively
A $\sqrt{45} and {tan}^{- 1} (\frac{1}{2})$
B $\sqrt{45} and {tan}^{- 1} (\frac{1}{3})$
C $\sqrt{75} and {tan}^{- 1} (2)$
D $\sqrt{75} and {tan}^{- 1} (\frac{1}{3})$
Four simple harmonic vibrations
$x_{1} = 8 s in (ω t), x_{2} = 6 sin (ω t + \frac{π}{2})$ ,
$x_{3} = 4 sin (ω t + π)$ and $x_{4} = 2 sin (ω t + \frac{3 π}{2})$ are superimposed on each other. The resulting amplitude is……units.
A $20$
B $8 \sqrt{2}$
C $4 \sqrt{2}$
D $4$
A vibratory motion is represented by $x = 2 A cos ω t + A cos (ω t + \frac{π}{2}) + A cos (ω t + π) + \frac{A}{2} cos (ω t + \frac{3 π}{2})$ .
the resultant amplitude of the motion is
A $\frac{9 A}{2}$
B $\frac{\sqrt{5} A}{2}$
C $\frac{5 A}{2}$
D2A

Recommended Questions

Home
Ask Doubt
Profile