A particle oscillates according to the law
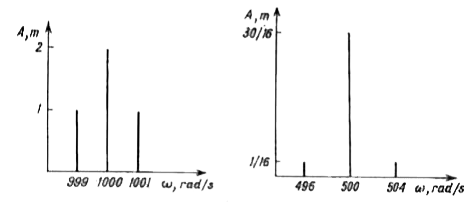
$s = 4 ({cos}^{2} 0.5 t) (sin 1000 t)$
Expand this motion into a harmonics series and plot its spectrum.

Text Solution

Verified by Experts

The correct Answer is:Hint. Write the product of the sinusoidal functions as a sum.

Carry out the following transformations:

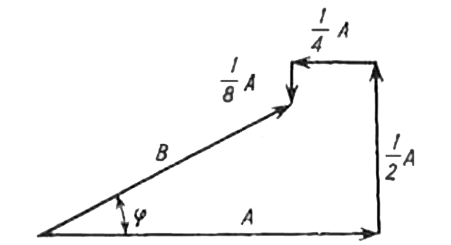
$s = 4 {cos}^{2} \frac{t}{2} . sin 1000 t = 2 (1 + cos t) sin 1000 t = 2 sin 1000 t + 2 sin 1000 t . cos t = 2 sin 1000 t + sin 1001 t - sin 999 t$
The spectrum is shown if Fig

|

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Similar Questions

Knowledge Check

Question 1 - Select One
A particle oscillates with S.H.M. according to the equation $x = 10 cos (2 π t + \frac{π}{4})$ . Its acceleration at $t = 1.5 s$ is
A $69.78 m s^{- 2}$
B $139.56 m s^{- 2}$
C $279.12 m s^{- 2}$
D0
Question 2 - Select One or More
A particle moves along the x-axis according to the equation $x = a sin ω t + b cos ω t$ . The motion is simple harmonic with
Atime period $2 π / ω$
Bamplitude $\sqrt{a^{2} + b^{2}}$
Camplitude a+b
Damplitude a-b
Question 3 - Select One
A particle moves along the $X$ -axis according to to the law $S = a {sin}^{2} (ω t - π / 4)$
The time period of oscillations is
A $\frac{2 π}{w}$
B $T / W$
C $\frac{3 π}{2 W}$
D $\frac{π}{2 W}$

Recommended Questions

Home
Ask Doubt
Profile