Prove that a photon in a vacuum, no matter how high its energy is, cannot transform to an electron-positron pair.
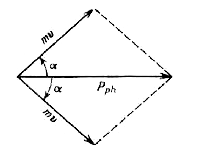
Suppose that the photon produces a pair of particles with identical momenta. In this case the laws of conservation of energy and the momentum will be writen in the form
εph=2mc2,εph/c=2mvcosα
Hence 2mc2=2mvccosα,orc=vcosα, which is impossible.
Similar Questions
What is the minimum energy released in the annhilation of an electron positron pair?
View Solution(a) The rest mass energy of an electron is m0c2=0.51MeV. Can a photon of this energy create an electron in free space?
(A) A single photon of energy 2m0c2 or greater has enough energy to form an electron (e−). Positron (e+) pair. But prove that this process cannot occur in free space.
(c) The pair production is possibel in presence of a third particle. Assume that a photon having frequency v collides with a nucleus of rest mass M0 (at rest) and creates an e−,e+ pair at rest. Calculate the mass M0 of the nucleus.
Neglect relativistic effect in all questions.
View Solution
Knowledge Check
The miniumum amount of energy released in annihilation of electron-Positron is
A1.02MeVB0.58MeVC185MeVD200MeVA gamma ray photon creates an electron positron pair if the rest mass energy of an electron is 0.5MeV and the total KE of the electron positron pair is 0.78 MeV then the energy of the gamma ray photon must be
A0.78 MeVB1.78 MeVC1.28MevD0.28MeVA gamma ray photon creates an electron positron pair if the rest mass energy of an electron is 0.5MeV and the total KE of the electron positron pair is 0.78 MeV then the energy of the gamma ray photon must be
A0.78 MeVB1.78 MeVC1.28MevD0.28MeV
Prove that a free electron at rest in a vacuum cannot absorb a photon.
View SolutionProve that an electron moving unfirmly in a straigght line in a vacuum cannot emit a photon.
View SolutionWhat is the minimum energy which a gamma ray photon must possess in order to produce electron positron pair ?
View SolutionIn an accelerator experiment on high energy collision of electrons with positrons, a certain events is interpreted as annihilation of an electron-positron pair of total energy 10.2 BeV into two γ-rays of equal energy. What is the wavelength associated with each γ-rays? (1BeV=109eV)
View SolutionIn an accelerator experiment on high energy collision of electrons with positrons, a certain events is interpted as annhilation of an electron-positron pair of total energy 10.2 BeV into two γ-rays of equal energy. What is the wavelength associated with each γ-rays? (1BeV=109eV)
View Solution
