If b and c are the lengths of the segments of any focal chord of a parabola $y^{2} = 4 a x$ , then length of the semi-latus rectum is:

A

$\frac{b + c}{2}$

B

$\frac{b c}{b + c}$

C

$\frac{2 b c}{b + c}$

D

$\sqrt{b c}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

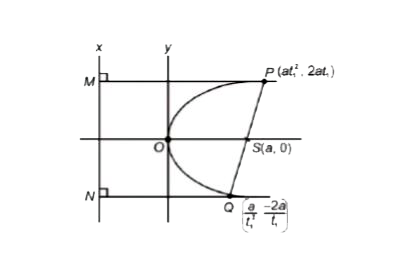
Let $P (a t_{1}^{2}, 2 a t_{1}) and Q (a t_{2}^{2}, 2 a t_{2})$ are end points of a chord
PQ is a focal chord
$t_{1} t_{2} = - 1$
$t_{2} = \frac{- 1}{t_{1}}$
$Q (\frac{a}{t_{1}^{2}}, \frac{- 2 a}{t_{1}})$
$b = S P = P M = a + a t_{1}^{2}$
$b - a = a t_{1}^{2} ... ... ... . . (i)$
$c = S Q = Q N = a + \frac{a}{t_{1}^{2}}$
$c - a = \frac{a}{t_{1}^{2}} ... ... ... . . (i i)$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
If b and c are the lengths of the segments of any focal chord of a parabola $y^{2} = 4 a x$ , then the length of the semi-latus rectum is
A $\frac{b + c}{2}$
B $\frac{b c}{b + c}$
C $\frac{2 b c}{b + c}$
D $\sqrt{b c}$
Question 2 - Select One
If b and k are segments of a focal chord of the parabola $y^{2} = 4 a x$ , then k =
A $\frac{a b}{b - a}$
B $\frac{b}{b - a}$
C $\frac{a}{b - a}$
D $\frac{a b}{a - b}$
Question 3 - Select One
The harmonic mean of the segments of a focal chord of the parabola $y^{2} = 16 a x,$ is
A2a
B4a
C8a
D16a

Recommended Questions

Home
Ask Doubt
Profile