The density of the earth is given by ρ=KgxryGz. Obtain the values of x,y and z
The correct Answer is:x=1,y=−1,z=−1
To solve the problem of finding the values of x, y, and z in the equation for the density of the Earth given by ρ=kgxryGz, we will follow these steps:
Step 1: Write down the dimensions of each variable
The density ρ has the dimension of mass per unit volume, which is given by:
(ρ)=ML−3
where M is mass and L is length.
The dimensions of the other variables are:
- Gravitational acceleration g:
(g)=LT−2
- Radius r:
(r)=L
- Gravitational constant G:
(G)=M−1L3T−2
Step 2: Substitute the dimensions into the equation
We can substitute the dimensions into the equation:
ρ=kgxryGz
This gives us:
ML−3=k(LT−2)x(L)y(M−1L3T−2)z
Step 3: Expand the right-hand side
Expanding the right-hand side:
ML−3=k⋅LxT−2x⋅Ly⋅M−zL3zT−2z
Combining the terms:
ML−3=k⋅M−z⋅Lx+y+3z⋅T−2x−2z
Step 4: Compare dimensions on both sides
Now we will compare the dimensions of both sides:
1. For mass M:
1=−z⇒z=−1
2. For length L:
−3=x+y+3z
Substituting z=−1:
−3=x+y+3(−1)⇒−3=x+y−3⇒x+y=0
3. For time T:
0=−2x−2z
Substituting z=−1:
0=−2x−2(−1)⇒0=−2x+2⇒2x=2⇒x=1
Step 5: Solve for y
Now substituting x=1 into the equation x+y=0:
1+y=0⇒y=−1
Final Values
Thus, we have:
x=1,y=−1,z=−1
Summary
The values of x, y, and z are:
- x=1
- y=−1
- z=−1
The density ρ has the dimension of mass per unit volume, which is given by:
(ρ)=ML−3
where M is mass and L is length.
- Gravitational acceleration g:
(g)=LT−2
- Radius r:
(r)=L
- Gravitational constant G:
(G)=M−1L3T−2
We can substitute the dimensions into the equation:
ρ=kgxryGz
This gives us:
ML−3=k(LT−2)x(L)y(M−1L3T−2)z
Expanding the right-hand side:
ML−3=k⋅LxT−2x⋅Ly⋅M−zL3zT−2z
Combining the terms:
ML−3=k⋅M−z⋅Lx+y+3z⋅T−2x−2z
Now we will compare the dimensions of both sides:
1. For mass M:
1=−z⇒z=−1
2. For length L:
−3=x+y+3z
Substituting z=−1:
−3=x+y+3(−1)⇒−3=x+y−3⇒x+y=0
3. For time T:
0=−2x−2z
Substituting z=−1:
0=−2x−2(−1)⇒0=−2x+2⇒2x=2⇒x=1
Now substituting x=1 into the equation x+y=0:
1+y=0⇒y=−1
Thus, we have:
x=1,y=−1,z=−1
The values of x, y, and z are:
- x=1
- y=−1
- z=−1
Topper's Solved these Questions
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM DERIVATION OF FORMULAE USING DIMENSIONS)
Explore 5 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CHECKING THE CORRECTNESS OF AN EQUATION)
Explore 13 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
- DYNAMICSBook:ICSEChapter:DYNAMICSExercise:SHORT ANSWER QUESTIONS WITH ANSWERS
Explore 12 Videos
Similar Questions
In dimension of critical velocity vc liquid following through a take are expressed as (ηxρyrz) where η,ρandrare the coefficient of viscosity of liquid, density of liquid and radius of the tube respectively then the value of x,y and z are given by
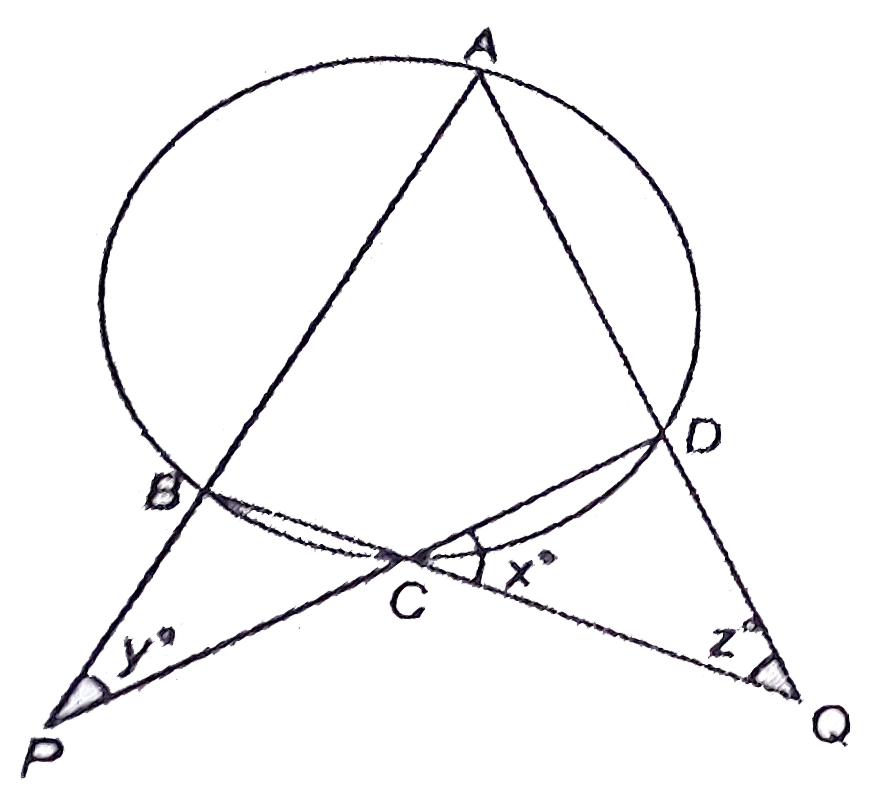
View SolutionIn given fig., if x3=y4=z5 , then calculate the values of x,y and z.
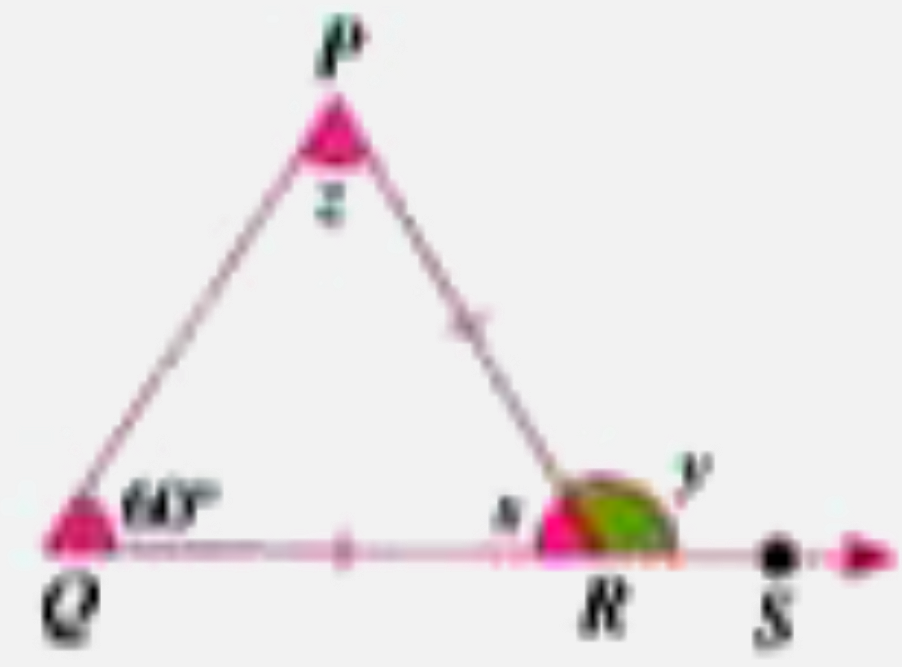
View SolutionFind the values of x,y and z in the given figure.
View SolutionGiven 3[xyzw]−[x6−12w]+[4x+yz+w3] , find the values of x, y, z and w.
View SolutionIf x, y, z are distinct positive numbers such that x+1y=y+1z=z+1x, then the value of xyz is __________
View SolutionIf x,y,z∈[−1,1] such that cos−1x+cos1y+cos−1z=3π, then find the values of (1) xy+yz+zy and (2) x(y+z)+y(z+x)+z(x+y)
View SolutionIf x,y,z∈[−1,1] such that cos−1x+cos1y+cos−1z=3π, then find the values of (1). xy+yz+zy and (2).x(y+z)+y(z+x)+z(x+y)
View SolutionIf x,y,z∈[−1,1] such that cos−1x+cos1y+cos−1z=3π, then find the values of (1) xy+yz+zx and (2) x(y+z)+y(z+x)+z(x+y)
View SolutionLet x,y,z∈R such that x+y+z=6andxy+yz+zx=7. Then find the range of values of x,y,andz.
View SolutionLet x,y,z be the vector, such that |x|=|y|=|z|=√2 and x,y,z make angles of 60∘ with each other. If x×(y×z)=a.
The value of y is:
View Solution