Given the sequence a, ab, aab, aabb, aaabb,aaabbb,…. Upto 2004 terms, the total number of times a's and b' s are used from 1 to 2004 terms are :
The correct Answer is:1002×1003a'sand(1002)2b's
To solve the problem of finding the total number of times 'a' and 'b' are used in the given sequence up to 2004 terms, we can break it down into a step-by-step solution.
Step 1: Understand the Sequence
The sequence is as follows:
1. a
2. ab
3. aab
4. aabb
5. aaabb
6. aaabbb
7. ...
From the pattern, we can see that:
- The nth term consists of 'a's followed by 'b's.
- The number of 'a's in the nth term is equal to the number of 'b's in the (n-1)th term plus 1.
- The number of 'b's in the nth term is equal to the number of 'b's in the (n-1)th term plus the number of 'a's in the (n-1)th term.
Step 2: Count the Number of 'a's
To find the total number of 'a's used from the 1st term to the 2004th term:
- The number of 'a's in each term can be represented as:
- Term 1: 1 'a'
- Term 2: 1 'a'
- Term 3: 2 'a's
- Term 4: 2 'a's
- Term 5: 3 'a's
- Term 6: 3 'a's
- ...
The pattern shows that:
- For every two terms, the number of 'a's increases by 1.
To find the total number of 'a's up to the 2004th term:
- There are 2004 terms, which means there are 1002 pairs of terms.
- Each pair contributes 1 additional 'a' to the total count.
Thus, the total number of 'a's is:
Total 'a's=1+1+2+2+3+3+...+1002=2×(1+2+3+...+1002)
Using the formula for the sum of the first n natural numbers:
Sum=n(n+1)2
Substituting n=1002:
Sum=1002×10032=502503
Thus, the total number of 'a's is:
Total 'a's=2×502503=1005006
Step 3: Count the Number of 'b's
To find the total number of 'b's used from the 1st term to the 2004th term:
- The number of 'b's in each term can be represented as:
- Term 1: 0 'b's
- Term 2: 1 'b'
- Term 3: 1 'b'
- Term 4: 2 'b's
- Term 5: 2 'b's
- Term 6: 3 'b's
- ...
From the pattern:
- For every two terms, the number of 'b's increases by 1.
Thus, the total number of 'b's is:
Total 'b's=0+1+1+2+2+3+3+...+1001
This can be calculated similarly:
- The total number of 'b's can be calculated as:
Total 'b's=1+2+3+...+1001=1001×10022=501501
Step 4: Final Count
Now, we can summarize:
- Total 'a's = 1005006
- Total 'b's = 501501
Thus, the total number of times 'a's and 'b's are used from the 1st to the 2004th term is:
Total=1005006+501501=1506507
Final Answer
The total number of times 'a's and 'b's are used from the 1st to the 2004th term is 1506507.
The sequence is as follows:
1. a
2. ab
3. aab
4. aabb
5. aaabb
6. aaabbb
7. ...
- The nth term consists of 'a's followed by 'b's.
- The number of 'a's in the nth term is equal to the number of 'b's in the (n-1)th term plus 1.
- The number of 'b's in the nth term is equal to the number of 'b's in the (n-1)th term plus the number of 'a's in the (n-1)th term.
To find the total number of 'a's used from the 1st term to the 2004th term:
- The number of 'a's in each term can be represented as:
- Term 1: 1 'a'
- Term 2: 1 'a'
- Term 3: 2 'a's
- Term 4: 2 'a's
- Term 5: 3 'a's
- Term 6: 3 'a's
- ...
The pattern shows that:
- For every two terms, the number of 'a's increases by 1.
- There are 2004 terms, which means there are 1002 pairs of terms.
- Each pair contributes 1 additional 'a' to the total count.
Total 'a's=1+1+2+2+3+3+...+1002=2×(1+2+3+...+1002)
Using the formula for the sum of the first n natural numbers:
Sum=n(n+1)2
Substituting n=1002:
Sum=1002×10032=502503
Thus, the total number of 'a's is:
Total 'a's=2×502503=1005006
To find the total number of 'b's used from the 1st term to the 2004th term:
- The number of 'b's in each term can be represented as:
- Term 1: 0 'b's
- Term 2: 1 'b'
- Term 3: 1 'b'
- Term 4: 2 'b's
- Term 5: 2 'b's
- Term 6: 3 'b's
- ...
- For every two terms, the number of 'b's increases by 1.
Total 'b's=0+1+1+2+2+3+3+...+1001
This can be calculated similarly:
- The total number of 'b's can be calculated as:
Total 'b's=1+2+3+...+1001=1001×10022=501501
Now, we can summarize:
- Total 'a's = 1005006
- Total 'b's = 501501
Total=1005006+501501=1506507
The total number of times 'a's and 'b's are used from the 1st to the 2004th term is 1506507.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -1 PART -II RMO3videos
SEQUENCE & SERIES
- BOOK - RESONANCECHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART -I PREVIOUS ASKED QUESTION FOR PRE RMO)18videos
SEQUENCE & SERIES
- BOOK - RESONANCECHAPTER - SEQUENCE & SERIES EXERCISE - SELF PRACTICE PROBLEMS22videos
SEQUENCE & SERIES
- BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - SSP55videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY37videos
TEST PAPER
Similar Questions
Knowledge Check
- Question 1 - Select One
There is a certain sequence of positive real numbers. Beginning from the third term, each term of the sequence is the sum of all the previous terms. The seventh term is equal to 1000 and the first term is equal to 1. The second term of this sequence is equal to
A246B1232C1234D124 - Question 2 - Select One
The bar chart given below shows the number of students (in '00) in a schoool from year 2000 to year 2004.
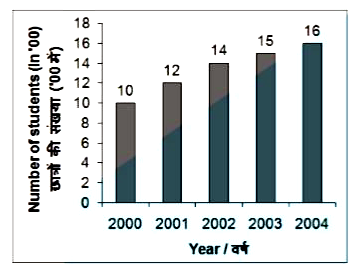
What is the total number of students in year 2002 and 2003?AA)2900BB)2700CC)3100DD)2800 - Question 3 - Select One
What is the respective ratio of total number of candidates clearing the entrance exam from stateB in the year 2004 to those clearing the entrance exam from state C in the same year?
 A221:148B218:143C148:221D143:218
A221:148B218:143C148:221D143:218
If there are 50 mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? (Use b for the number of boxes.)
View SolutionGiven a sequence of 4 numbers, first three of which are in G.P. and the last three are in arcommon difference six. If first and last terms of this sequence are equal, then the last term is (A) 8(B) 16(C) 2 .(D) 4
View SolutionFind four consecutive terms in an A.P. Whose sum is 72 and the ratio of the product of the 1st and the 4th terms to the product of the 2nd and 3rd terms is 9 : 10.
(a) Let the four consecutive terms be a - 3d, a - d, a + d, a + 3d.
(b) Using the first condition, find the value of a.
(c) Using the second condition, find the value of d and hence the numbers.View SolutionStudy the following graph carefully and answer the question given below.
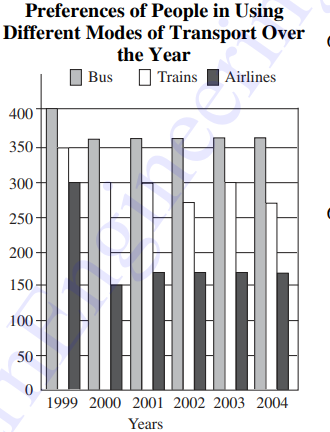 From 1999 to 2004, the total number of people who preferred to travel by trains, was approximately how many millions? View Solution
From 1999 to 2004, the total number of people who preferred to travel by trains, was approximately how many millions? View SolutionThe two given expressions on either side of the ‘=’ sign will have the same value if two terms on either side or on the same side are interchanged. Find from the given option the correct terms to be interchanged.
View Solution

