Vector →A is 2cm long and is 600 above the x-axis in the first quadrant, vector →B is 2cm long and is 600 below the x-axis in the fourth quadrant. Find →A+→B.
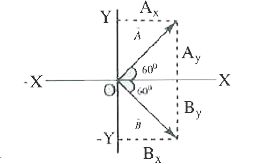
→R=→A+→B
→R=2cos600ˆi+2sin60ˆj+2cos60ˆi−2sin60ˆj
→R=4cos60ˆi=2ˆi
:.2cm, along x-axis
Similar Questions
Vector →A is 2 cm long and is 60° above the x - axis in the first quadrant, vector →B is 2cm long and is 60° below the x - axis in the fourth quadrant. Find →A+→B
View SolutionVector →A is 2cm long and is 60∘ above the x-axis in the first quadrant. Vactor →B is 2cm long and is 60∘ below the x-axis in the fourth quadrant. The sum →A+→B is a vector of magnitudes
View Solution
Knowledge Check
Vector →A is 2cm long and is 60∘ above the x-axis in the first quadrant. Vector →B is 2cm long and is 60∘ below the x-axis in the fourth quadrant. The sum →A+→B is a vector of magnitudes
A2cm along positive y-axisB2cm along positive x-axisC2cm along negative y-axisD2cm along negative x-axisA vector →A is along the positive z-axis and its vector product with another vector →B is zero, then vector →B could be :
Aˆi+ˆjB4ˆiCˆi+ˆkD−7ˆkIf →A+→B is a unit vector along x-axis and →A=ˆi−ˆj+ˆk, then what is →B ?
Aˆi+ˆkBˆj−ˆkCˆi+ˆj+ˆkDˆi+ˆj−ˆk
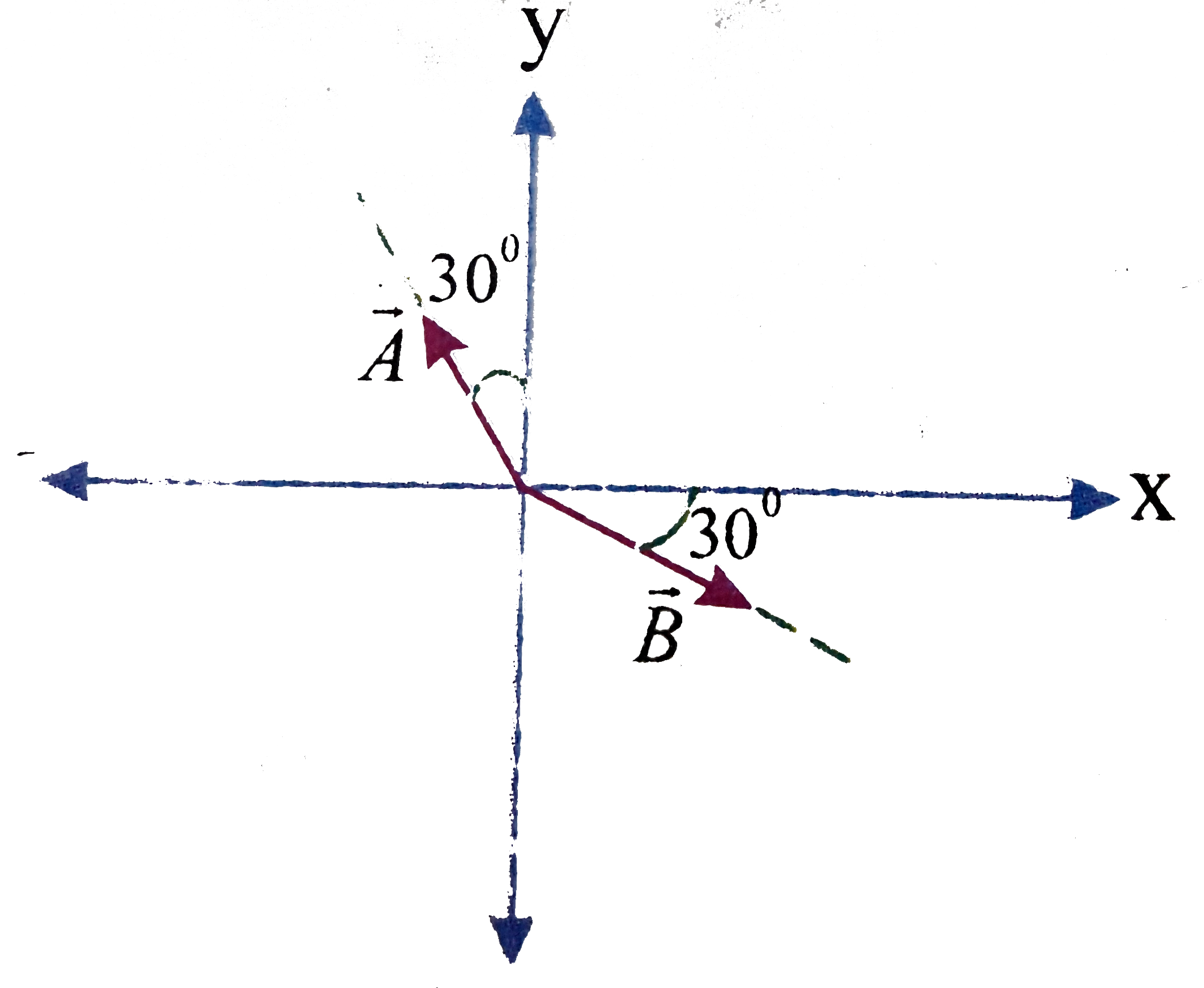
A vector →A makes an angle 30∘ with the Y-axis in anticlockwise direction. Another vector →B makes an angle 30∘ with the x-axis in clockwise direction. Find angle between vectors →A and →B.
View SolutionA vector →A is along the positive z-axis and its vector product with another vector →B is zero, then vector →B could be :
View SolutionVector →A has a magnitude of 6.00 vector →B has a magnitude of 7.00 units, and →A.→B has a value of 14.0 What is the angle between the direction of →Aand→B ?
View SolutionVector →A, which is directed along an x axis, is to be added to vector →B, which has a magnitude of 6.0 m. The sum is a third vector that is directed along the y axis, with a magnitude of →AFind the magnitude of →A ?
View SolutionIf →A+→B is a unit vector along x-axis and →A=ˆi−ˆj+ˆk, then what is →B?
View Solution
