What is the displacement of the point of a wheel initally in contact with the fround when the wheel rolls forward half a rervolution ? Take the radius of the wheel as R and the x-axis as he forward direction?
From figure, during half revolution of the wheel, the point A covers horizontal distance, and BC = 2R vertical distance.

x=iR and y =2R, Displacement,
and
with x-axis.
i.e., Displacement has magnitude and makes an angle with x-axis.
Similar Questions
What is the displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward half a revolution? Take the radius of the wheel as R and the x-axis as the forward direction?
View SolutionWhat is the displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward half a revolution ? Take the radius of the wheel as R and the the x - axis as the forward direction ?
View Solution
Knowledge Check
The displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward quarter revolution where perimeter of the wheel is 4πm, is (Assume the forward direction as x-axis)
A√(π+2)2+4along tan−12π with x-axisB√(π+2)2+4along tan−12π−2 with x-axisC√(π+2)2+4along tan−12π with x-axisD√(π+2)2+4along tan−12π−2 with x-axisA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
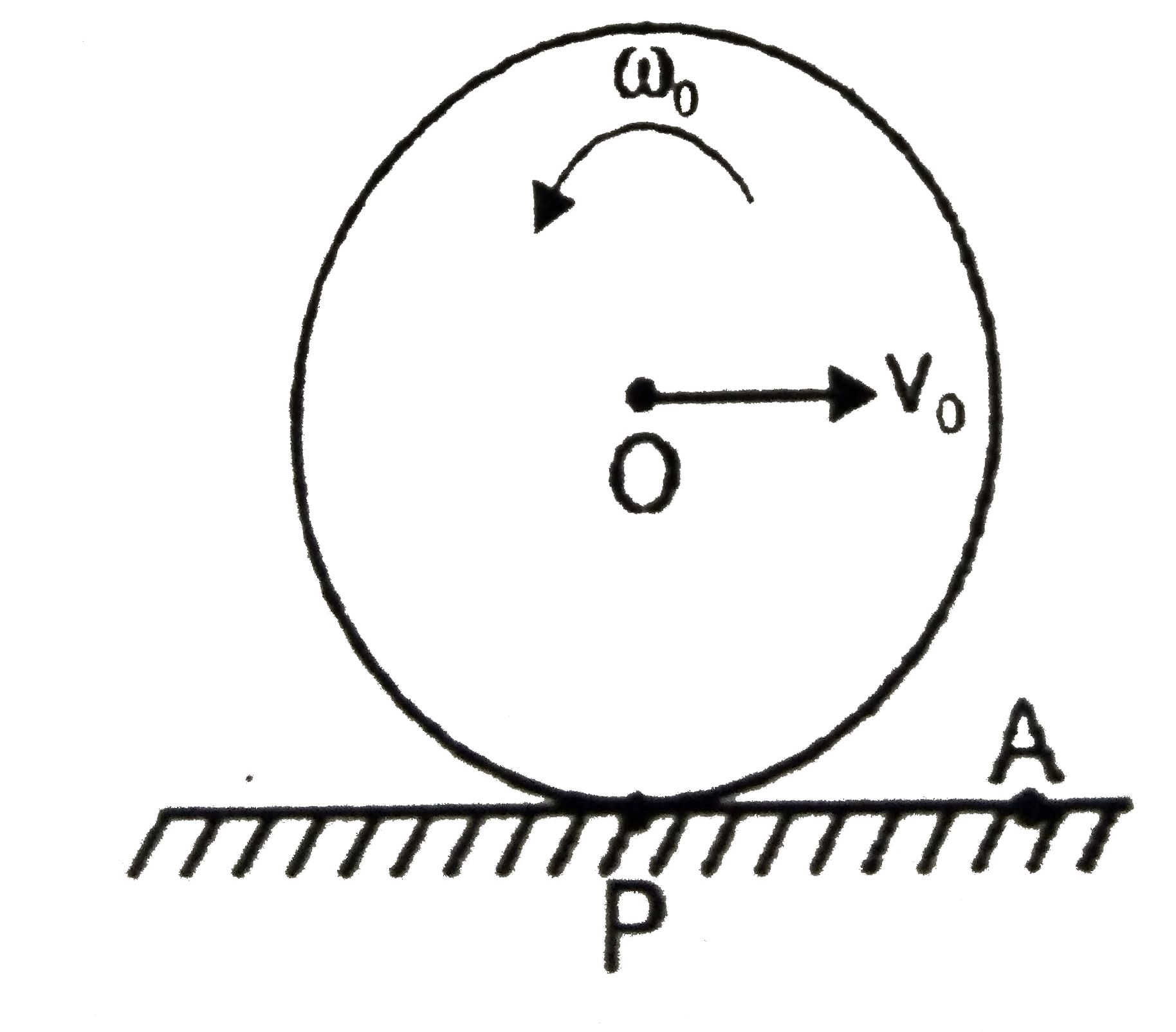
If above question , distance travelled by centre of mass of the wheel before it stops is −Av202μg(1+r2k2)Bv202μgCv202μg(1+k2r2)DNone of these
A Wheel of circumference C is at rest on the ground.When the wheel rolls forward through half a revolution ,then the displacement of point contact will be
View SolutionA wheel of circumference C is at rest on the ground. When the wheel rolls forward through half a revolution, then the displacement of initial point of contact will be
View SolutionA wheel of perimeter 4π is rolling on a horizontal surface. The displacement of the point of contact of wheel and ground when the wheel completes one quarter of revolution is
View SolutionIf a given point P is in contact with ground initially and wheel of radius R is in pure rolling, then the displacement of point P when point P reaches topmost of the sphere for the first time will be
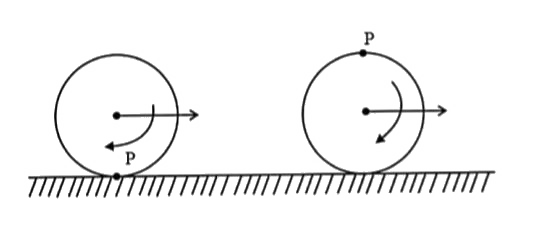
View SolutionIf a given point P is in contact with ground initially and wheel of radius R is in pure rolling, then the displacement of point P when point P reaches topmost of the sphere for the first time will be

View SolutionA stunt rider on a unicycle is riding around thearena of a circus in a circle of radius R. The radius of the wheel of the unicycle is r and the angular velocity with which the wheel rotates is ω. What is the angular acceleration of the wheel ? (Ignore the fact that the wheel axis is inclined.)
View Solution
