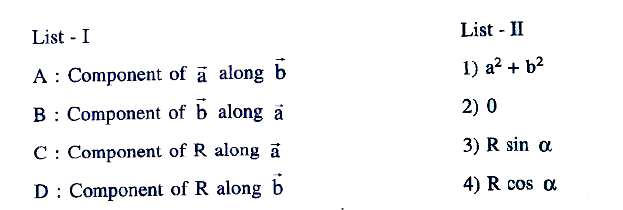
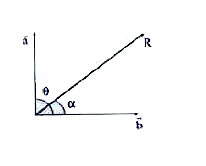
If veca and vecb are the two vectors vecR resultant of veca, vecb as s

If $\to a and \to b$ are two vector with $| \to a | = ∣ ∣ \to b ∣ ∣$ and $∣ ∣ \to a + \to b ∣ ∣ + 2 | \to a |$ ,then angle between $\to a$ and $\to b$ .
A $0^{\circ}$
B $90^{\circ}$
C $60^{\circ}$
D $180^{\circ}$
If $\to a and \to b$ are othogonal unit vectors, then for a vector $\to r$ non - coplanar with $\to a and \to b$ vector $\to r \times \to a$ is equal to
A $[\to r \to a \to b] \to b - (\to r . \to b) (\to b \times \to a)$
B $[\to r \to a \to b] (\to a + \to b)$
C $[\to r \to a \to b] \to a + (\to r . \to a) \to a \times \to b$
Dnone of these

If $\to a and \to b$ are the two vectors $\to R$ resultant of $\to a, \to b$ as shown