(A) : Relative velocity is zero when two bodies are moving opposite to each other with same velocity
( R) : Relative velocity of a body does not depend on direction of motion.
Both (A) and ( R) are ture and ( R) is the correct explanation of (A)
Both (A) and ( R) are true and ( R) is not the correct explanation of (A)
(A) is true but ( R) is false
Both (A) and ( R) are false
The correct Answer is:D
Similar Questions
The escape velocity of a body does not depend on the mass of the body.
View Solution(A): Relative velocity of A w.r.t. B is greater than the velocity of either, when they are moving in opposite directions.
(R): The relative velocity between any two bodies is equal to the sum of the velocities of the two bodies.
View Solution
Knowledge Check
Two bodies are moving in opposite direction with speed V. What is the magnitude of their relative velocity ?
A.0,BV,CY2D2V.Statement-1 : The relative velocity between any two bodies moving in opposite direction is equal to sum of the velocities of two bodies. Statement-2 : Sometimes relative velocity between two bodies is equal to difference in velocities of the two.
AIf both assertion and reason are trure and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanations of assertion.CIf assertion is true but reason is false.DIf both assertion and reason is falseThe vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A train A moves to the east with velocity of 40 km/hr and a train B moves due north with velocity of 30 km/hr. The relative velocity of A w.rt. B is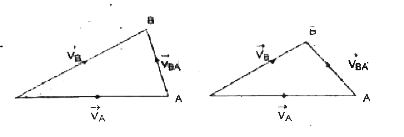
A70 km/hr towards EastB10 km/hr towards North EastC50 km/hr at some angle South of EastD50 km/hr at some angle North of East.
Statement-1 : The relative velocity between any two bodies moving in opposite direction is equal to sum of the velocities of two bodies. Statement-2 : Sometimes relative velocity between two bodies is equal to difference in velocities of the two.
View SolutionStatement-1 : The velocity of a body A relative to the body B is the sum of the velocities of bodies A and B if both travel in opposite direction on a straight line.
Statement-2 : The velocity of a body A relative to the body B is the difference of the velocities of bodies A and B if both travel in opposite direction on a straight line.
View SolutionThe vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A train A moves to the east with velocity of 40 km/hr and a train B moves due north with velocity of 30 km/hr. The relative velocity of A w.rt. B is
View SolutionTwo cars are moving is one a same line dimension in opposite direction with the same speed v. The relative velocity of two cars w.r.t. each other is
View SolutionAssertion: Relative velocity of A w.r.t B is greater than the velocity of either, when they are moving in opposite directions.
Reason: Relative velocity of A w.r.t B=→vA−→vB
View Solution