Figure shows three vectors →a,→band→c, where R is the midpoint of PQ. Then which of the following relations is correct?
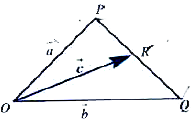
→a+→b=2→c
→a+→b=→c
→a−→b=2→c
→a−→b=→c
The correct Answer is:A
Similar Questions
Figure shows three vectors →a,→b and →c. If ¯¯¯¯¯¯RQ=2¯¯¯¯¯¯PR, which of the following relation is correct :-
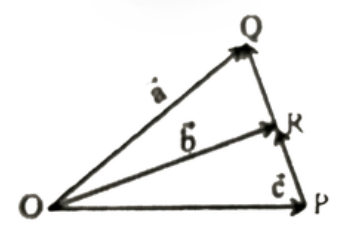
View SolutionIf →a,→band→c are three vectors of which every pair is non colinear. If the vector →a+→band→b+→c are collinear with the vector →c and →a respectively then which one of the following is correct? (A) →a+→b+→c is a nul vector (B) →a+→b+→c is a unit vector (C) →a+→b+→c is a vector of magnitude 2 units (D) →a+→b+→c is a vector of magnitude 3 units
View Solution
Knowledge Check
Figure shows three vectors →a,→b and →c where R is the mid point of PQ, then which of the following relations is correct.
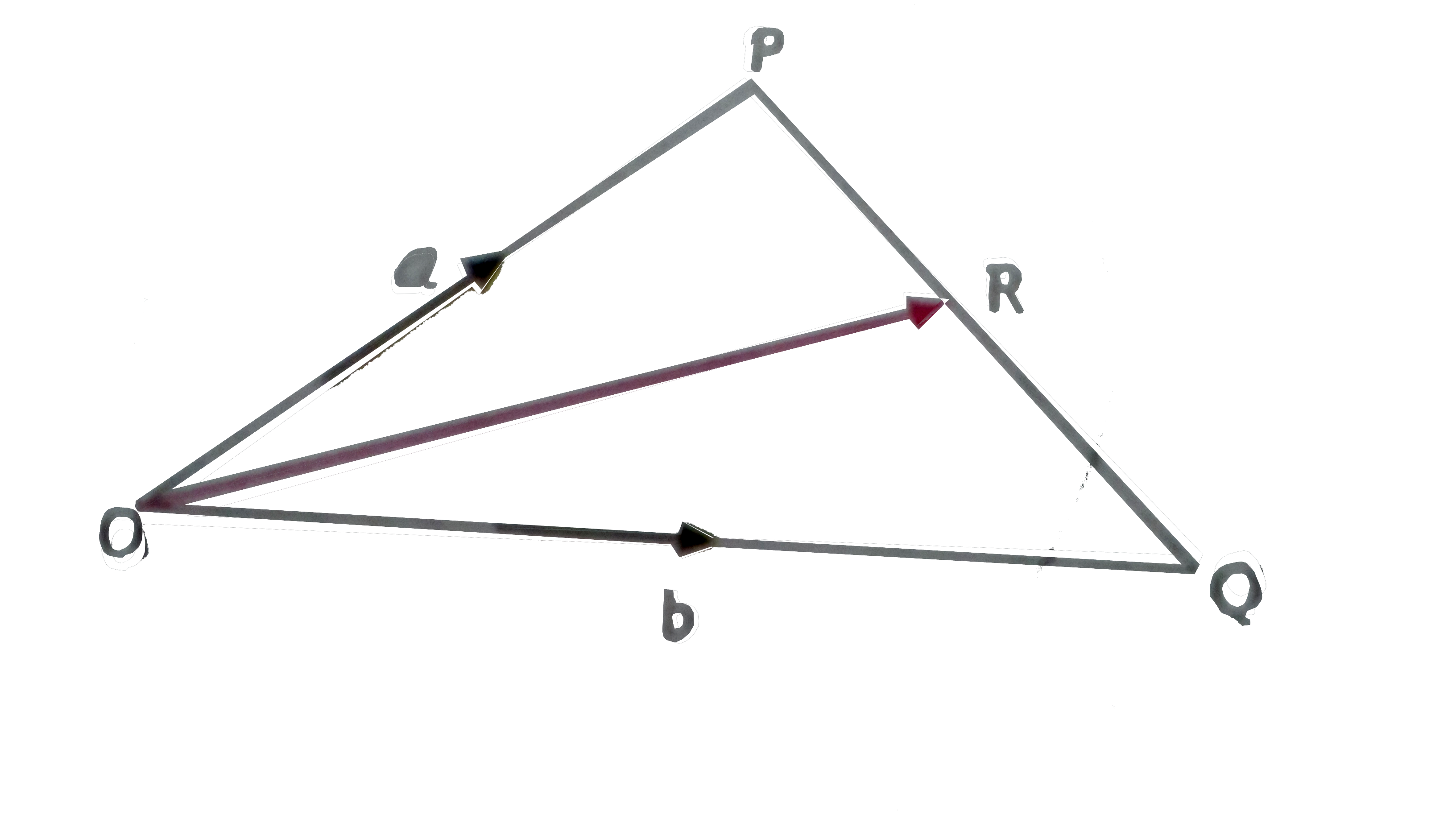 A→a+→b=2→cB→a+→b=→cC→a−→b=2→cD→a−→b=→c
A→a+→b=2→cB→a+→b=→cC→a−→b=2→cD→a−→b=→cFigure shows three vectors →a,→b and →c, where R is the midpoint of PQ. Then which of the following relations is correct?
 A→a+→b=2→cB→a+→b=→cC→a−→b=2→cD→a−→b=→c
A→a+→b=2→cB→a+→b=→cC→a−→b=2→cD→a−→b=→cThree vectors →a,→b and →c satisfy the relation →a.→b=0 and →a.→c=0. The vector →a is parallel to
A→bB→C must be less than ∣∣→A−→B∣∣C→b.→cD→b×→c
If →a,→band→c are three vectors of which every pair is non colinear. If the vector →a+→band→b+→c are collinear with the vector →c and →a respectively then which one of the following is correct? (A) →a+→b+→c is a nul vector (B) →a+→b+→c is a unit vector (C) →a+→b+→c is a vector of magnitude 2 units (D) →a+→b+→c is a vector of magnitude 3 units
View SolutionConsider three vectors →A,→Band→C as shown in fig. perform graphically the following vector additions and subtractions (a) →A+→B
(b). →A+→B+→C
(c). →A−→B
(d). →A+→B−→C

View SolutionLet →a,→b,→c be unit vectors such that →a+→b+→c=→0. Which of the following is correct?
View Solutionfor any three vectors, →a,→band→c,(→a−→b).(→b−→c)×(→c−→a) =
View SolutionThree vectors →A,→B and →C satisfy the relation →A.→B=0 and →A.→C=0. The vector →A is parallel to
View Solution
