The number of lines of symmetry of a circle is
0
1
4
unlimited
The correct Answer is:d
To determine the number of lines of symmetry of a circle, we can follow these steps:
1. Understanding the Circle:
- A circle is a round shape where every point on the boundary is equidistant from the center.
Hint: Remember that the center of the circle is the point from which all points on the circumference are equally distant.
2. Defining Lines of Symmetry:
- A line of symmetry is a line that divides a shape into two identical halves that are mirror images of each other.
Hint: Think of folding a shape along a line; if both halves match perfectly, that line is a line of symmetry.
3. Drawing Lines Through the Center:
- When we draw a line through the center of the circle, it divides the circle into two equal parts. This line is called a diameter.
Hint: Visualize or sketch a circle and draw a line through the center; notice how both sides are equal.
4. Identifying Multiple Lines:
- Since a circle has a center, we can draw an infinite number of lines through this center at various angles. Each of these lines will also bisect the circle into two equal halves.
Hint: Imagine rotating a line around the center of the circle; every position creates a new line of symmetry.
5. Conclusion:
- Therefore, the number of lines of symmetry in a circle is infinite.
Hint: Remember that because you can draw lines at any angle through the center, there is no limit to the number of symmetrical divisions.
Final Answer:
The number of lines of symmetry of a circle is infinite.
- A circle is a round shape where every point on the boundary is equidistant from the center.
- A line of symmetry is a line that divides a shape into two identical halves that are mirror images of each other.
- When we draw a line through the center of the circle, it divides the circle into two equal parts. This line is called a diameter.
- Since a circle has a center, we can draw an infinite number of lines through this center at various angles. Each of these lines will also bisect the circle into two equal halves.
- Therefore, the number of lines of symmetry in a circle is infinite.
The number of lines of symmetry of a circle is infinite.
Similar Questions
Knowledge Check
The number of lines of symmetry of a rectangle is
A0B1C2D4The number of lines (s) of symmetry of a line segment is
A0B1C2Dinfinite.The number of lines of symmetry of a scalene triangles is
A0B1C2D3
The number of lines of symmetry of an isosceles triangle is (a) 0 (b) 1 (c) 2 (d) 3
View SolutionThe number of lines of symmetry of an equilateral triangle is (a) 1 (b) 2 (c) 3 (d) 0
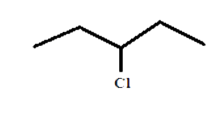
View SolutionDetermine the number of planes of symmetry of the given compound
View SolutionDraw all possible lines of symmetry in each of the following figures and state the number of lines of symmetry in each case.

View SolutionThe number of lines of symmetry which a triangle cannot have is
View Solution
