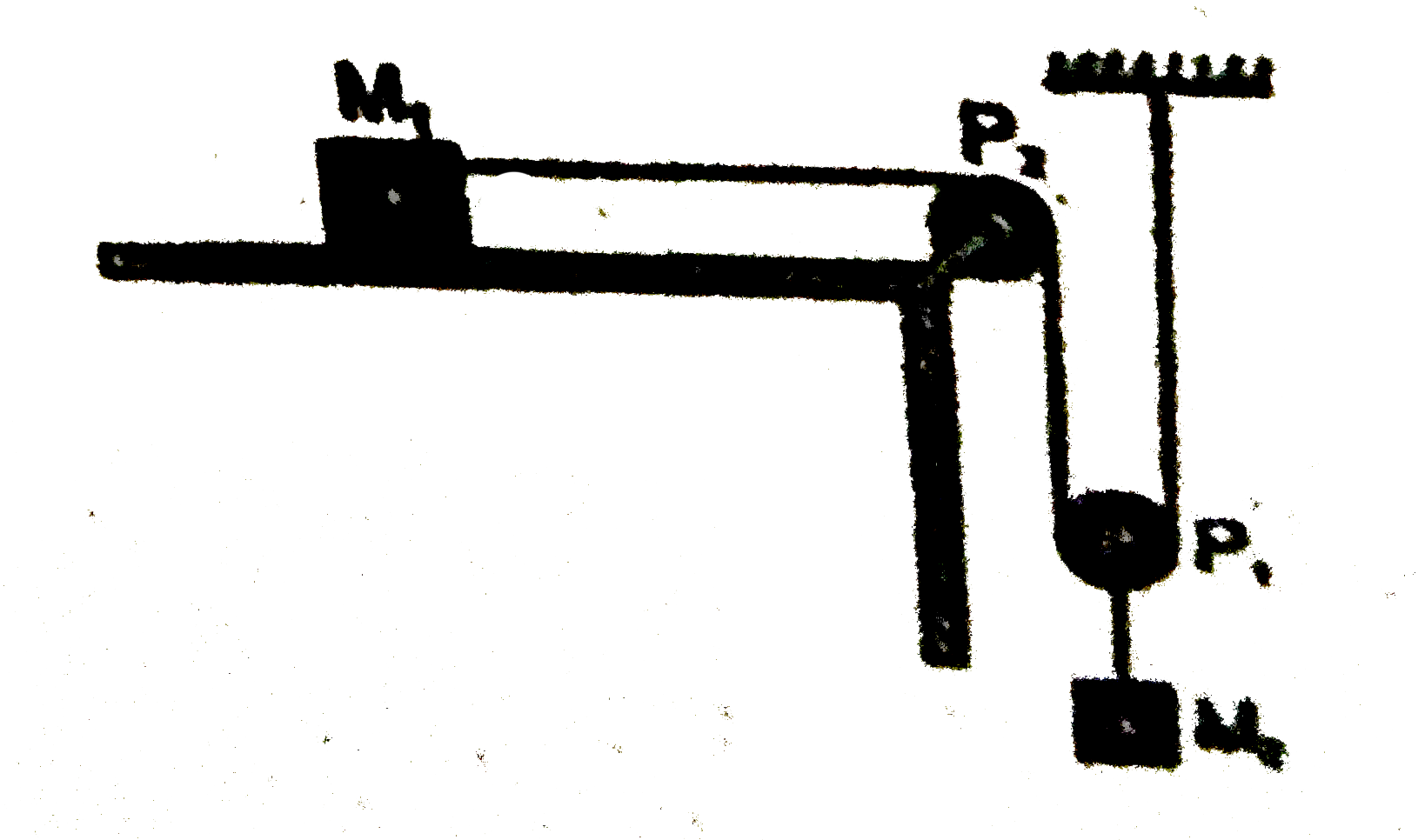
Masses M1 , M2 and M3 are connected by strings of negligible mass which pass over massless and frictionless pulleys P1 and P2 as shown in the fig. The masses move such that the portion of the string between P1 and P2 is parallel to the incline and the portion of the string between P2 and M3 is horizontal. The masses M3 and M2 are 4.0kg each and the coefficient of kinetic friction between the masses and the surface is 0.25. The inclined plane makes an angle of 37∘ with the horizontal. Find the mass M1.

Let the tension between the masses M1 and M2 be T1 and that between M2 and M3 be T2. The kinetic friction between the masses and the surface is the μk. The equations of motion for different masses are,
T1−T2−μkM2gcosθ=M2gsinθ
T1=M1g
M1g−T2−μkM2gcosθ−M2gsinθ=0
M1×9.8−9.8−0.25×4×9.8×cos37−4×9.8×sin37=0
9.8M1−9.8−7.82−23.59=0
9.8M1=41.21
M1=4.205kg
Topper's Solved these Questions
- BOOK - ICSECHAPTER - FRICTIONEXERCISE - Conceptual short answer questions with answer9videos
FRICTION
- BOOK - ICSECHAPTER - FRICTIONEXERCISE - Long answer questions2videos
FRICTION
- BOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems30videos
FRICTION
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS12videos
DYNAMICS
- BOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP2videos
GRAVITATION
Similar Questions
Masses M1,M2andM3 are connected by string of negligible mass which pass over massless and frictionless pulleys P1andP2 as shown in figure 7.15. The masses move such that the string between P1andP2 is parallel to the incline and the portion of the string between P2andM3 is horizontal. The masses M2andM3 are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfces is 0.25. The inclined plane makes an angle of 37∘ with the horizontal. If the mass M1moves downwards with a uniform velocity, find (i) the mass of M1, (ii) the tension in the horizontal portion. (g=9.8ms−2,sin37∘=35)
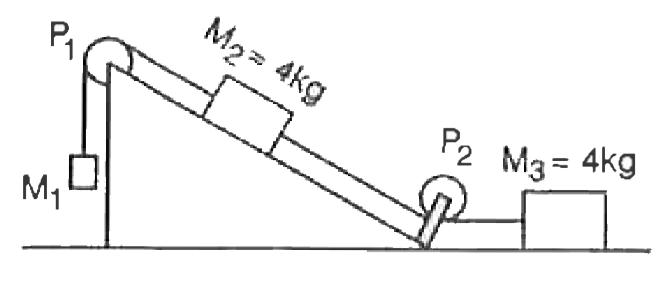 View Solution
View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
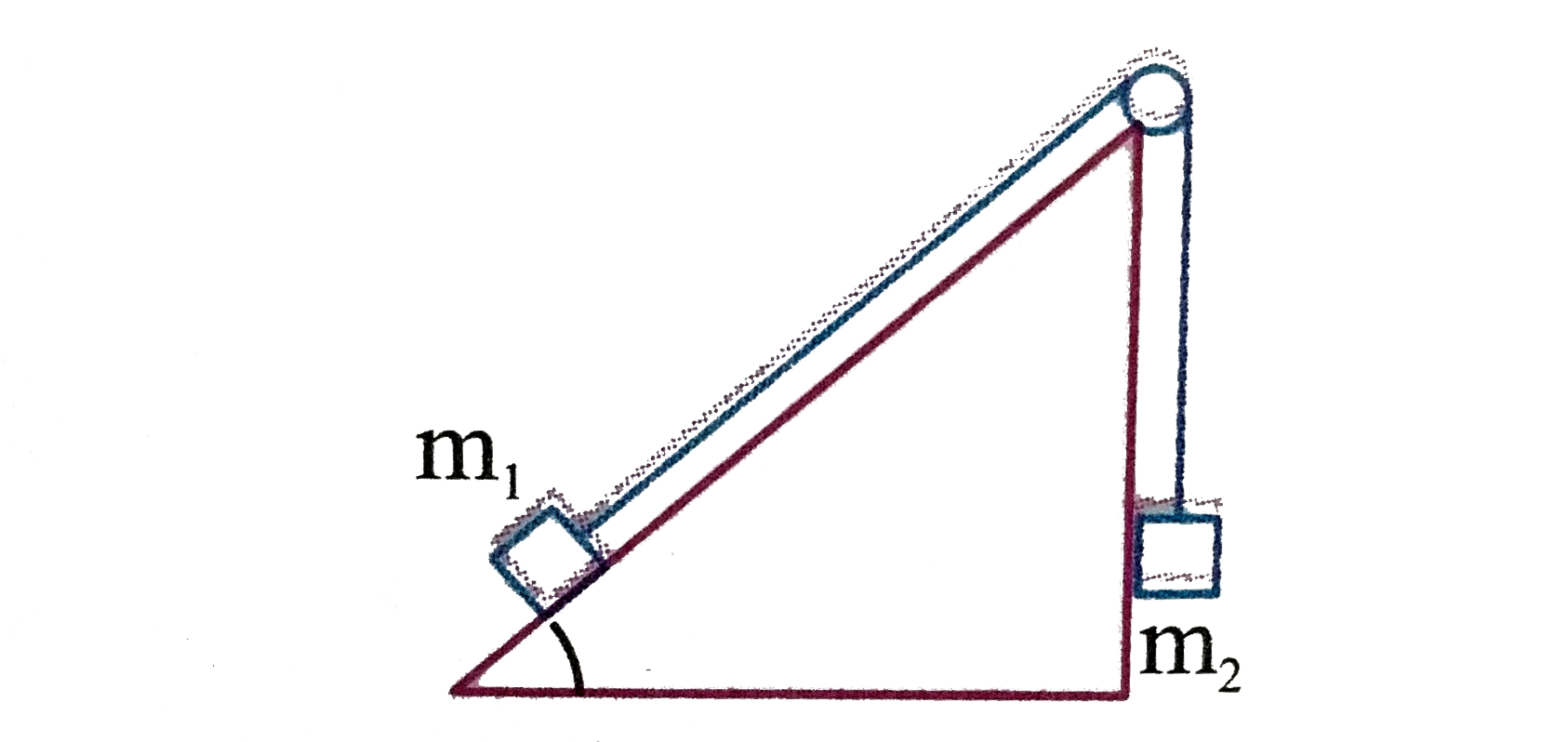 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A string of negligible mass going over a clamped pulley of mass m supports a block of M as shown in the figure. the force on the pulley by the clamp is given by:
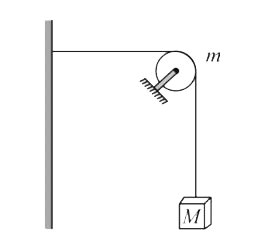 A√2MgB√2mgC√(M+m)2+m2gD√(M+m)2+M2g
A√2MgB√2mgC√(M+m)2+m2gD√(M+m)2+M2g - Question 2 - Select One
A string of negligible mass going over a clamped pulley of mass M as shown in Fig. 3.14. The force on pulley by the clamb is given by
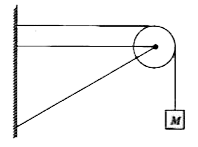 A2 mgB√2 mgC√{(M+m)2+m2} gD√{(M+m)2+M2} g
A2 mgB√2 mgC√{(M+m)2+m2} gD√{(M+m)2+M2} g
Blocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
 View Solution
View SolutionA string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by
 View Solution
View SolutionThree masses m1=m,m2=2mandm3=3m are hund on a string passing over a frictionless pulley as shown in Figure . The mass of the string in negligible . The system is released from rest.
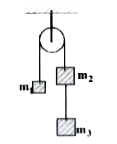
The tension in the string between masses m1andm2 isView SolutionTwo masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is
 View Solution
View SolutionThree masses m1=m,m2=2mandm3=3m are hund on a string passing over a frictionless pulley as shown in Figure . The mass of the string in negligible . The system is released from rest.
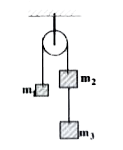
The tension in the string between masses m2andm3 isView SolutionTwo masses M1=5kg, M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
(a) g (b) g2 (c) g3 (d) g4
 View Solution
View Solution
