Obtain an expression for the period of oscillations of a mass attached to end of a spring and undergoing shm. Obtain expression for K.E. and P.E. at any position during shm.
To derive the expressions for the period of oscillation of a mass attached to a spring undergoing Simple Harmonic Motion (SHM), as well as the expressions for kinetic energy (K.E.) and potential energy (P.E.) at any position during SHM, we can follow these steps:
Step 1: Understanding the System
We have a mass m attached to a spring with spring constant k. When the mass is displaced from its equilibrium position, the spring exerts a restoring force that causes the mass to oscillate.
Step 2: Applying Hooke's Law
According to Hooke's Law, the restoring force F exerted by the spring is proportional to the displacement y from the mean position:
F=−ky
where k is the spring constant and y is the displacement.
Step 3: Relating Force to Acceleration
Using Newton's second law, we know that:
F=ma
where a is the acceleration. Since acceleration is the second derivative of displacement with respect to time, we can write:
F=md2ydt2
Setting the two expressions for force equal gives:
md2ydt2=−ky
Step 4: Formulating the Differential Equation
Rearranging the equation, we have:
d2ydt2+kmy=0
This is a standard form of the differential equation for SHM.
Step 5: Identifying Angular Frequency
The general solution to this equation indicates that the motion is harmonic, and we can identify the angular frequency ω:
ω2=km
Thus, the angular frequency ω is:
ω=√km
Step 6: Finding the Time Period
The time period T of the oscillation is related to the angular frequency by:
T=2πω
Substituting for ω:
T=2π√mk
Step 7: Expression for Potential Energy (P.E.)
The potential energy stored in the spring when it is displaced by y is given by:
P.E.=12ky2
Step 8: Expression for Kinetic Energy (K.E.)
The kinetic energy of the mass when it is at position y can be derived from its velocity. The velocity v of the mass in SHM is given by:
v=ω√A2−y2
where A is the amplitude of the motion. The kinetic energy is then:
K.E.=12mv2=12m(ω2(A2−y2))
Substituting ω2=km:
K.E.=12k(A2−y2)
Summary of Results
1. Time Period:
T=2π√mk
2. Potential Energy:
P.E.=12ky2
3. Kinetic Energy:
K.E.=12k(A2−y2)
We have a mass m attached to a spring with spring constant k. When the mass is displaced from its equilibrium position, the spring exerts a restoring force that causes the mass to oscillate.
According to Hooke's Law, the restoring force F exerted by the spring is proportional to the displacement y from the mean position:
F=−ky
where k is the spring constant and y is the displacement.
Using Newton's second law, we know that:
F=ma
where a is the acceleration. Since acceleration is the second derivative of displacement with respect to time, we can write:
F=md2ydt2
Setting the two expressions for force equal gives:
md2ydt2=−ky
Rearranging the equation, we have:
d2ydt2+kmy=0
This is a standard form of the differential equation for SHM.
The general solution to this equation indicates that the motion is harmonic, and we can identify the angular frequency ω:
ω2=km
Thus, the angular frequency ω is:
ω=√km
The time period T of the oscillation is related to the angular frequency by:
T=2πω
Substituting for ω:
T=2π√mk
The potential energy stored in the spring when it is displaced by y is given by:
P.E.=12ky2
The kinetic energy of the mass when it is at position y can be derived from its velocity. The velocity v of the mass in SHM is given by:
v=ω√A2−y2
where A is the amplitude of the motion. The kinetic energy is then:
K.E.=12mv2=12m(ω2(A2−y2))
Substituting ω2=km:
K.E.=12k(A2−y2)
1. Time Period:
T=2π√mk
2. Potential Energy:
P.E.=12ky2
3. Kinetic Energy:
K.E.=12k(A2−y2)
Topper's Solved these Questions
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SHORT ANSWER QUESTIONS
Explore 47 Videos
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:VERY SHORT ANSWER QUESTIONS
Explore 13 Videos
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SHORT ANSWER QUESTIONS WITH ANSWER
Explore 20 Videos
- MOTION IN FLUIDS Book:ICSEChapter:MOTION IN FLUIDS Exercise:SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
Explore 19 Videos
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
Explore 12 Videos
Similar Questions
Write down the expression for the period of oscillation of a mass attached to (i) a horizontal spring and (ii) a vertical spring.
View SolutionDerive an expression for the P.E. and K.E. of a body executing shm.
View SolutionDerive an experession for the period of oscillation of a mass attached to a spring executing simple harmonic motion. Given that the period of oscillation depends on the mass m and the force constant k, where k is the force required to stretch the spring by unit length?
View SolutionIs oscillation of a mass suspended by a spring simple harmonic ? give expression for its time period also.
View SolutionAt what displacement K.E. and P.E. are equal, for a body executing shm.
View SolutionObtain an expression for intensity of electric field in end on position, i.e., axial position of an electric dipole.
View SolutionOne end of an ideal spring is fixed to a wall at origin O and axis of spring is parallel to x-axis. A block of mass m=1kg is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is x=10+3sin(10t). Here, t is in second and x in cm. Another block of mass M=3kg, moving towards the origin with velocity 30cm/s collides with the block performing SHM at t=0 and gets stuck to it. Calculate

(a) new amplitude of oscillations,
(b) neweqution for position of the combined body,
( c) loss of energy during collision. Neglect friction.
View SolutionOne end of an ideal spring is fixed to a wall at origin O and axis of spring is parallel to x-axis. A block of mass m=1kg is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is x=10+3sin(10t). Here, t is in second and x in cm. Another block of mass M=3kg, moving towards the origin with velocity 30cm/s collides with the block performing SHM at t=0 and gets stuck to it. Calculate
(a) new amplitude of oscillations,
(b) new equation for position of the combined body,
( c) loss of energy during collision. Neglect friction.
View Solution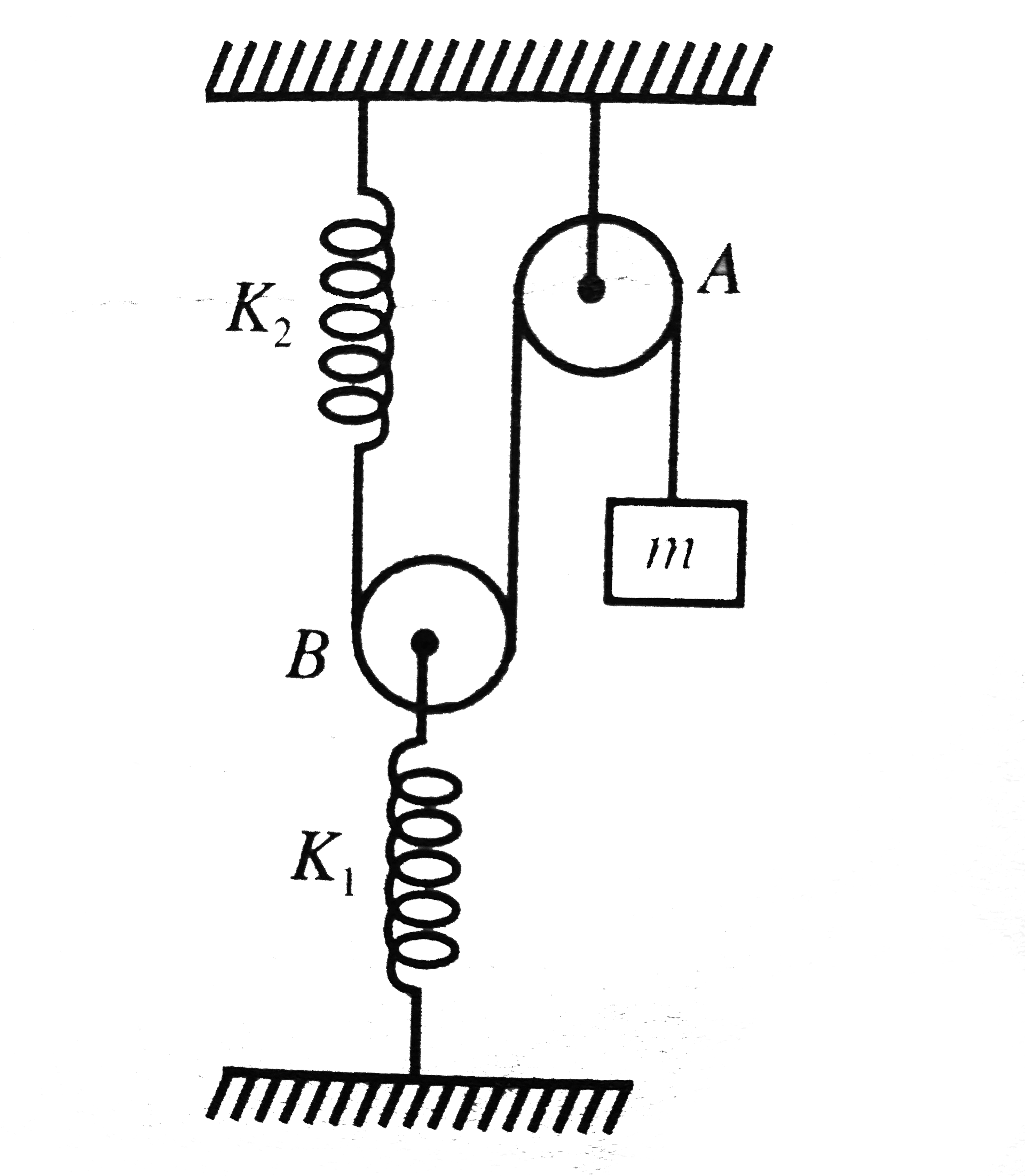
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)
View SolutionThere are two ideal springs of force constants K1 and K2 respectively. When both springs are relaxed the separation between free ends is L. Now the particle of mass m attached to free end of left spring is displaced by distance 2L towards left and then released. assuming the surface to be frictionless. (K1K2=43). (Neglect size of the block)
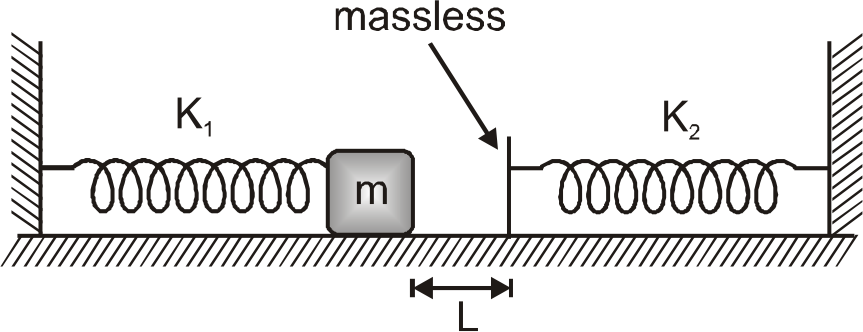
Suppose mass m hits the right spring and sticks to it. The extension in left spring when mass ‘m’ is in equilibrium position during its motion is :
View Solution