One litre of an ideal gas at a pressure of 6 atm undergoes an adiabatic expansion until its pressure drops to one atmosphere and volume increases to 2 litre. Find the word done during the process.
To find the work done during the adiabatic expansion of an ideal gas, we can use the formula for work done in an adiabatic process:
W=1γ−1(P1V1−P2V2)
where:
- W = work done
- P1 = initial pressure
- V1 = initial volume
- P2 = final pressure
- V2 = final volume
- γ = heat capacity ratio (given as 1.4)
Step 1: Convert the given values to SI units.
- Initial volume V1=1L=1×10−3m3
- Final volume V2=2L=2×10−3m3
- Initial pressure P1=6atm=6×1.013×105Pa
- Final pressure P2=1atm=1.013×105Pa
Step 2: Calculate the pressures in Pascals.
- P1=6×1.013×105=6.078×105Pa
- P2=1.013×105Pa
Step 3: Substitute the values into the work done formula.
W=11.4−1((6.078×105Pa)×(1×10−3m3)−(1.013×105Pa)×(2×10−3m3))
Step 4: Calculate the terms inside the parentheses.
- First term: 6.078×105×1×10−3=607.8J
- Second term: 1.013×105×2×10−3=202.6J
Step 5: Calculate the difference.
607.8J−202.6J=405.2J
Step 6: Substitute into the work done formula.
W=10.4×405.2J=1013J
Thus, the work done during the process is:
W=1013J
---
- W = work done
- P1 = initial pressure
- V1 = initial volume
- P2 = final pressure
- V2 = final volume
- γ = heat capacity ratio (given as 1.4)
- Initial volume V1=1L=1×10−3m3
- Final volume V2=2L=2×10−3m3
- Initial pressure P1=6atm=6×1.013×105Pa
- Final pressure P2=1atm=1.013×105Pa
- P1=6×1.013×105=6.078×105Pa
- P2=1.013×105Pa
W=11.4−1((6.078×105Pa)×(1×10−3m3)−(1.013×105Pa)×(2×10−3m3))
- First term: 6.078×105×1×10−3=607.8J
- Second term: 1.013×105×2×10−3=202.6J
607.8J−202.6J=405.2J
W=10.4×405.2J=1013J
W=1013J
Topper's Solved these Questions
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SOLVED EXAMPLES9videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - ADDITIONAL SOLVED PROBLEMS12videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP2videos
GRAVITATION
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)19videos
MOTION IN FLUIDS
Similar Questions
An ideal gas of volume 1 litre and at a pressure 8 atm undergoes an adiabatic expansion until its pressure drops to 1 atm and volume increase to 4 liters. Calculate the work done in the process (y = 1.5).
View SolutionIf a gas at a pressure of 10atm at 300K expands against a constant external pressure of 2atm from a vol. 10 litres to 20 litres find work done ? [Isothermal process]
View Solution
Knowledge Check
- Question 1 - Select One
1 mole of an ideal gas at STP is subjected to a reversible adiabatic expansion to double its volume. Find the change in internal energy (γ=1.4)
A1169 JB769 JC1374 JD969 J - Question 2 - Select One
Two litres of an ideal gas at a pressure of 10 atm expands isothermally at 25∘C into a vacuum until its total volume is 10 litres. How much heat is absorbed and how much work is done in the expansion ?
A10 J, 10 JB8 J, 10 JC18 J, 0 JD0 J, 0 J
An ideal gas at a pressure of 1 atm and temperature of 27∘C is compressed adiabatically until its pressure becomes 8 times the initial pressure , then final temperature is (γ=32)
View SolutionA gas present at 5 atm pressure expands against one atmosphere when its volume changes from 3 litre to 5 litre. The work done by the gas in Joule will be ?
View SolutionOne mole of an ideal monotomic gas undergoes a linear process from A to B in which its pressure p and its volume V change as shown in figure.
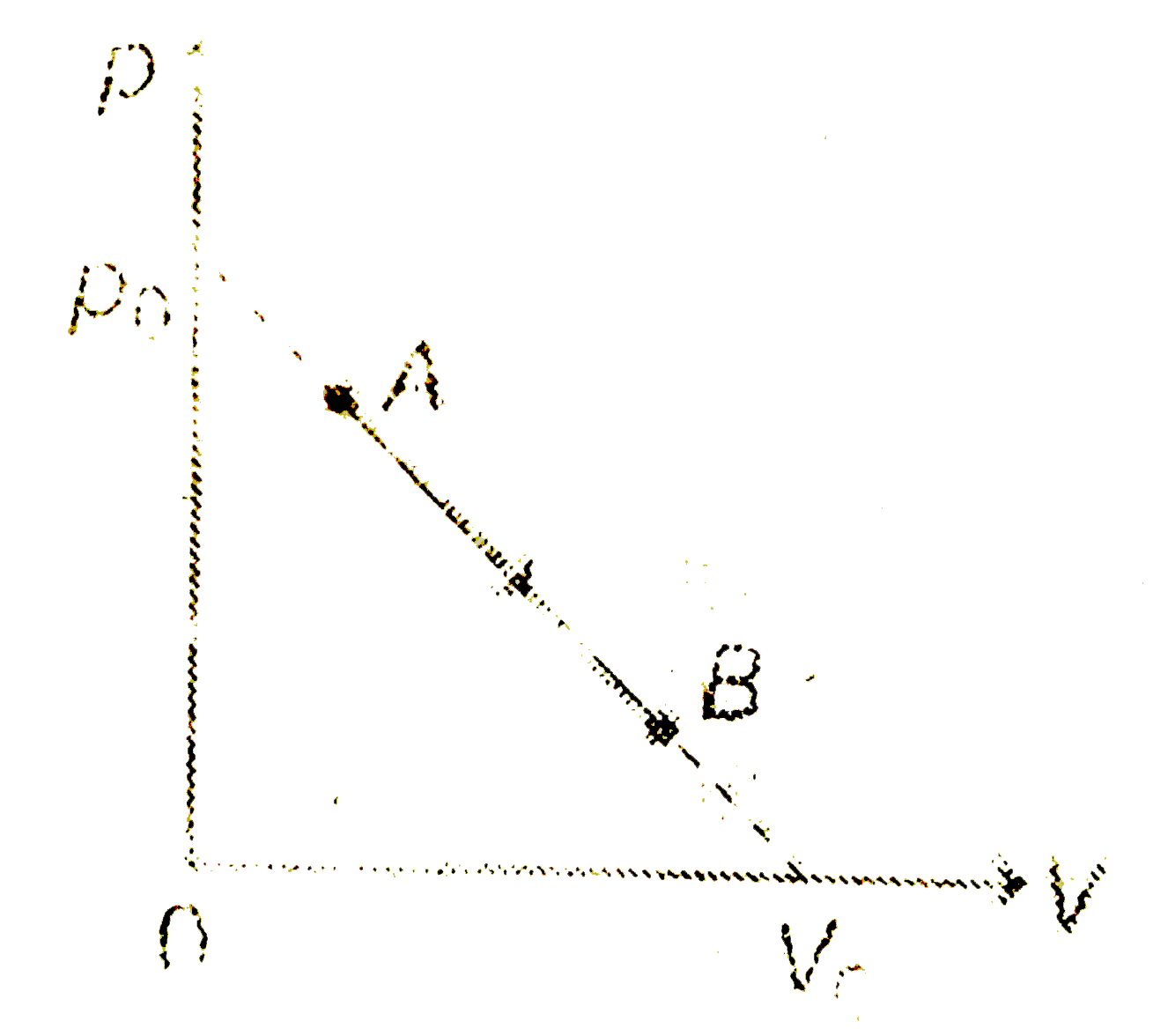
The maximum temperature of the gas during this process isView SolutionAn ideal gas occuping a volume of 2dm3 and a pressure of 5 bar undergoes isothermal and irreversible expansion against external pressure of 1 bar. The final volume of the system and work involved in the process is
View SolutionTwo litres of an ideal gas at a pressure of 10 atm expands isothermally at 25∘C into a vacuum until its total volume is 10 litres. How much heat is absorbed and how much work is done in the expansion ?
View SolutionAn ideal gas undergoes isothermal expansion at constant pressure . During the process.
View Solution

