Variation OF ΔHr and ΔUr Temperature [ KirchhOFf’s Equation ] || Variation OF ΔSr with P and T || Physical Significance OF Entropy || Third Law OF Thermodynamics and its Application
Step by step video solution for Variation OF ΔHr and ΔUr Temperature [ KirchhOFf’s Equation ] || Variation OF ΔSr with P and T || Physical Significance OF Entropy || Third Law OF Thermodynamics and its Application by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Variation of K with temperature as given by van't Hoff equation can be written as
AlogK2K1=−ΔH2.303R[1T1−1T2]BlogK2K1=ΔH2.303R[1T2−1T1]ClogK2K1=−ΔH2.303R[1T2−1T1]DNone of the aboveEnergy is associated with the orientation and distribution of molecules in space. Disordered crystals have higher entropy than ordered crystals and diffused gases have higher entropy than compressed gases.

Entropy is also associated with molecular motion. As the temperature of a substance increases, random molecular motion increases hence entropy increases. Figure gives variation of entropy with temperature. At absolute zero (−273∘C) every substance is in solid state whose particles are rigidly fixed in a crystalline structure. If there is no residual orientational disorder, like that in CO, entropy of the substance is zero. Third law of thermodynamics states.
At the absolute zero of temperature the entropy of every substance become zero and does become zero in case of perfectly crystalline structure.
understand(T→0)(LtS)=0
In case of CO and NO molecules in solid state, there is randomness even at 0K due to their dipole moments hence entropy in such cases is not zero even at 0K. As the temperature is raised, the molecules begin to vibrate. The number of ways in which the vibrational energy can be distributed increases with increases in temperature and the entropy of solid increases steadily as the temperature increaes. At the melting point (mp) of the solid, there is a discontinous jump in entropy because there are many more ways of arranging the molecules in the liquid than in the solid. An even greater jump in entropy is observed at the boiling point (bp) because molecules in the gas are to free to occupy a more larger volume and randomness increases.
Predict the sign of ΔS in the system for each of the following process
(I)CO2(s)→CO2(g)
(II)CaSO4(s)→CaO(s)+SO3(g)
(III)N2(g)+3H2(g)→2NH3(g)
(IV)I2(s)→I2(aq)AIIIIIIIV+ve+ve−ve+veBIIIIIIIV+ve−ve−ve+veCIIIIIIIV−ve−ve+ve+veDIIIIIIIV+ve−ve−ve−veEnergy is associated with the orientation and distribution of molecules in space. Disordered crystals have higher entropy than ordered crystals and diffused gases have higher entropy than compressed gases.
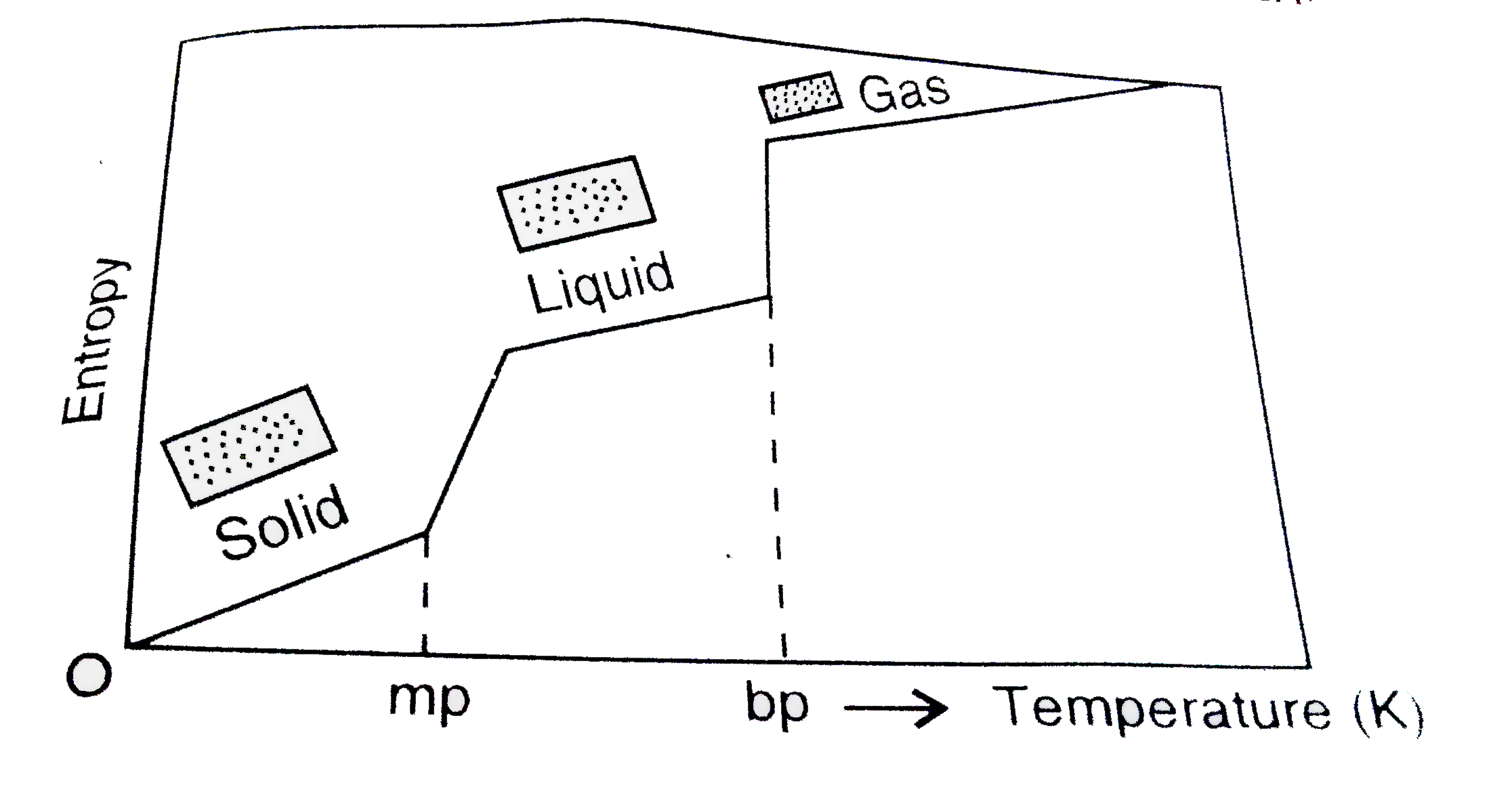
Entropy is also associated with molecular motion. As the temperature of a substance increases, random molecular motion increases hence entropy increases. Figure gives variation of entropy with temperature. At absolute zero (−273∘C) every substance is in solid state whose particles are rigidly fixed in a crystalline structure. If there is no residual orientational disorder, like that in CO, entropy of the substance is zero. Third law of thermodynamics states.
At the absolute zero of temperature the entropy of every substance become zero and does become zero in case of perfectly crystalline structure.
understand(T→0)(LtS)=0
In case of CO and NO molecules in solid state, there is randomness even at 0K due to their dipole moments hence entropy in such cases is not zero even at 0K. As the temperature is raised, the molecules begin to vibrate. The number of ways in which the vibrational energy can be distributed increases with increases in temperature and the entropy of solid increases steadily as the temperature increaes. At the melting point (mp) of the solid, there is a discontinous jump in entropy because there are many more ways of arranging the molecules in the liquid than in the solid. An even greater jump in entropy is observed at the boiling point (bp) because molecules in the gas are to free to occupy a more larger volume and randomness increases.
For the following reaction
CaCO3(s)→CaO(s)+CO2(g)
If at 0K, ΔS of this reaction is Xcalmol−1 then entropy of CO2(g) at 0K isA−XcalB−2XcalC+XcalD0cal
State third law of thermodynamics. Write applications of standard molar entropy.
View SolutionGibb’s Energy and Equilibrium Constant || Variation OF Keq with Temperature || T-S Diagram for Carnot Cycle || Physical Significance OF Gibb’s Energy
View Solution
Assertion: If variation in resistance due to temperature is taken into consideration, then current in the circuit I and power produced across the resistance P both will decrease with time.
Reason: V=IR is ohm's law.
View SolutionIn order to analyse variation of rate constant with temperature Arrhenius equation is used the two parameters involved pre-exponential factor and activation energy are assumed to be constant in the theory while in reality they may vary with temperature It is further observed that Arrhenius factor is proportional to √T and hence the equation can be restated as: k=A√Te−Ea/RT (where A' is temperature independent). However, for most of the analysis its variation is neglected Also, if activation energy is temperature dependent then Arrhenius equation does not hold true and the following equation should be used
dlnkdT=EaRT2
where symbols have usual meaning.
Assuming Arrhenius factor to be constant and activation energy to be dependent on temperature and varying as (0.02T2) cal (if T is in Kelvin scale) then calculate by what factor will rate constant increase if temperature is increased from 200 K to 400 K?
View SolutionIn order to analyse variation of rate constant with temperature Arrhenius equation is used the two parameters involved pre-exponential factor and activation energy are assumed to be constant in the theory while in reality they may vary with temperature It is further observed that Arrhenius factor is proportional to √T and hence the equation can be restated as: k=A√Te−Ea/RT (where A' is temperature independent). However, for most of the analysis its variation is neglected Also, if activation energy is temperature dependent then Arrhenius equation does not hold true and the following equation should be used
dlnkdT=EaRT2
where symbols have usual meaning.
For a reaction where activation energy is 800 cal, by what factor will rate constant increase if Arrhenius factor is assumed to be temperature dependent and temperature is changed from 200 K to 400 K?
View Solution
