The sum of the expression 551 + 552 + 553 + … + 560 is :
3450
5555
555
6060
The correct Answer is:B
To find the sum of the expression 551+552+553+…+560, we can recognize that this is an arithmetic progression (AP) where:
1. First term (A): 551
2. Common difference (D): 552−551=1
3. Last term: 560
Step 1: Determine the number of terms (n)
To find the number of terms in the series, we can use the formula for the n-th term of an arithmetic progression:
an=a+(n−1)d
Setting an=560, a=551, and d=1:
560=551+(n−1)⋅1
Subtract 551 from both sides:
560−551=n−1
9=n−1
Adding 1 to both sides gives:
n=10
Step 2: Use the formula for the sum of an arithmetic series
The formula for the sum Sn of the first n terms of an arithmetic progression is:
Sn=n2⋅(2a+(n−1)d)
Substituting the values we found:
- n=10
- a=551
- d=1
We can now substitute these values into the formula:
S10=102⋅(2⋅551+(10−1)⋅1)
Calculating step-by-step:
1. Calculate 2a:
2⋅551=1102
2. Calculate (n−1)d:
(10−1)⋅1=9
3. Add these results together:
1102+9=1111
4. Now substitute back into the sum formula:
S10=5⋅1111
5. Finally, calculate 5⋅1111:
5⋅1111=5555
Final Answer
Thus, the sum of the expression 551+552+553+…+560 is:
5555
2. Common difference (D): 552−551=1
3. Last term: 560
To find the number of terms in the series, we can use the formula for the n-th term of an arithmetic progression:
The formula for the sum Sn of the first n terms of an arithmetic progression is:
- a=551
- d=1
Thus, the sum of the expression 551+552+553+…+560 is:
Topper's Solved these Questions
Similar Questions
Knowledge Check
The sum of the rational expression x−3x2+1 and its reciprocal is
A2x2−6x+10x−3Bx4+3x2−6x+10x3−3x2+x−3Cx4+2x2−6x−10x3−3x2+x−3DNone of theseThe units digit of the expression 125813×5533703×4532828 is
A4B2C0D5The sum of the rational expression x−3x2+1 and its reciprocal is
A2x2−6x+10x−3Bx4+3x2−6x+10x3−3x2+x−3Cx4+2x2−6x−10x33x2+x−3DNone of these
What annual payment will discharge a debt of Rs 1025 due in 2 years at the rate of 5% compound interest? (a) Rs 550 (b) Rs 551.25 (c) Rs 560 (d) Rs 560.75
View SolutionFind the unit digit of expression 125^813 * 553^3703 * 4537^828?
View Solution212 : 436 :: 560 : ?
View SolutionFind the sum of n terms of the following expression.
8 + 88 + 888 + ........ ?
View Solution462 552 650 756 870 992 ?
View Solution

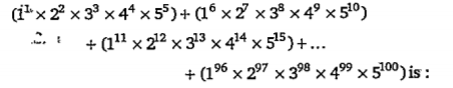 is:
is: