What is the maximum integral value of m, if n<0 and m = n+(285)/n ?
-34
-286
34
-33
The correct Answer is:A
To find the maximum integral value of m given that n<0 and m=n+285n, we can follow these steps:
Step 1: Rewrite the expression for m
We start with the equation:
m=n+285n
Step 2: Find the derivative to locate critical points
To maximize m, we can take the derivative of m with respect to n and set it to zero. However, since n must be negative, we can also analyze the function directly by substituting negative factors of 285.
Step 3: Identify factors of 285
The factors of 285 are:
- −1,−3,−5,−15,−19,−57,−95,−285
Step 4: Calculate m for each negative factor
We will calculate m for each negative factor of 285:
1. For n=−1:
m=−1+285−1=−1−285=−286
2. For n=−3:
m=−3+285−3=−3−95=−98
3. For n=−5:
m=−5+285−5=−5−57=−62
4. For n=−15:
m=−15+285−15=−15−19=−34
5. For n=−19:
m=−19+285−19=−19−15=−34
6. For n=−57:
m=−57+285−57=−57−5=−62
7. For n=−95:
m=−95+285−95=−95−3=−98
8. For n=−285:
m=−285+285−285=−285−1=−286
Step 5: Identify the maximum value of m
From the calculations above, the values of m for the negative factors of 285 are:
- −286,−98,−62,−34,−34,−62,−98,−286
The maximum integral value of m is:
Maximum m=−34
Conclusion
Thus, the maximum integral value of m is:
−34
We start with the equation:
m=n+285n
To maximize m, we can take the derivative of m with respect to n and set it to zero. However, since n must be negative, we can also analyze the function directly by substituting negative factors of 285.
The factors of 285 are:
- −1,−3,−5,−15,−19,−57,−95,−285
We will calculate m for each negative factor of 285:
m=−1+285−1=−1−285=−286
m=−3+285−3=−3−95=−98
m=−5+285−5=−5−57=−62
m=−15+285−15=−15−19=−34
m=−19+285−19=−19−15=−34
m=−57+285−57=−57−5=−62
m=−95+285−95=−95−3=−98
m=−285+285−285=−285−1=−286
From the calculations above, the values of m for the negative factors of 285 are:
- −286,−98,−62,−34,−34,−62,−98,−286
Maximum m=−34
Thus, the maximum integral value of m is:
−34
Topper's Solved these Questions
Similar Questions
Knowledge Check
A and B are any two sets, n(A)=17 and n(B)=13. What is the maximum possible value of n(A∪B)−n(A∩B) ?
A4B13C17D30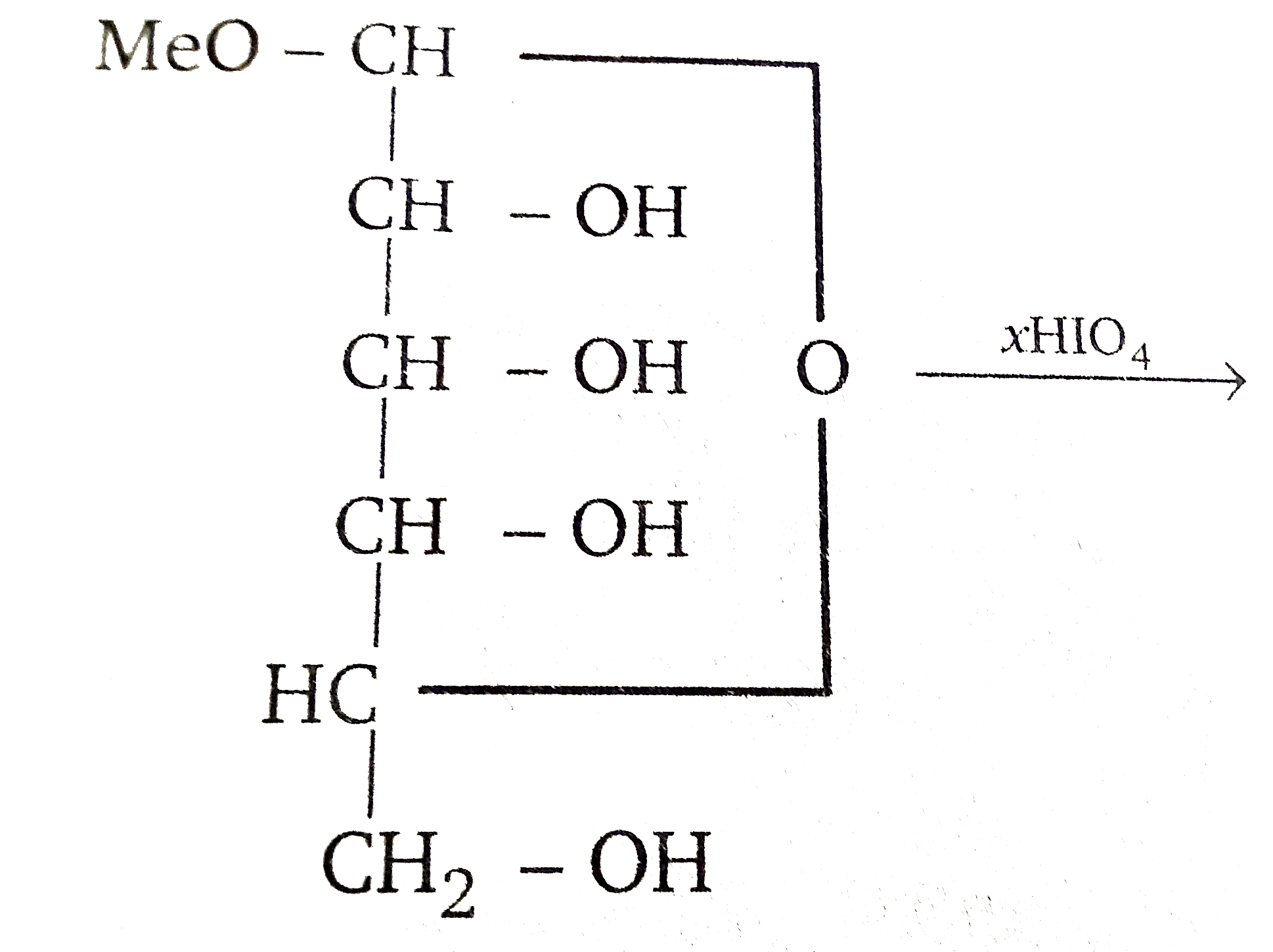 What is the maximum value of (x)?A1B2C3D4
What is the maximum value of (x)?A1B2C3D4What is the maximum value of sinθcosθ ?
A1B1/2C1/√2D√3/2
For what integral value of x is
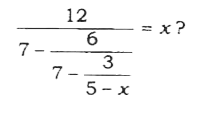
View SolutionIn the interhalogen compound ABn, what is the maximum value of n ?
View SolutionIf M&α are twin prime &α+M=7 then the greatest integral value of N is
View SolutionFind the maximum value (n+l+m) for unpaired electrons in second excited state of chlorine .17Cl.
View Solution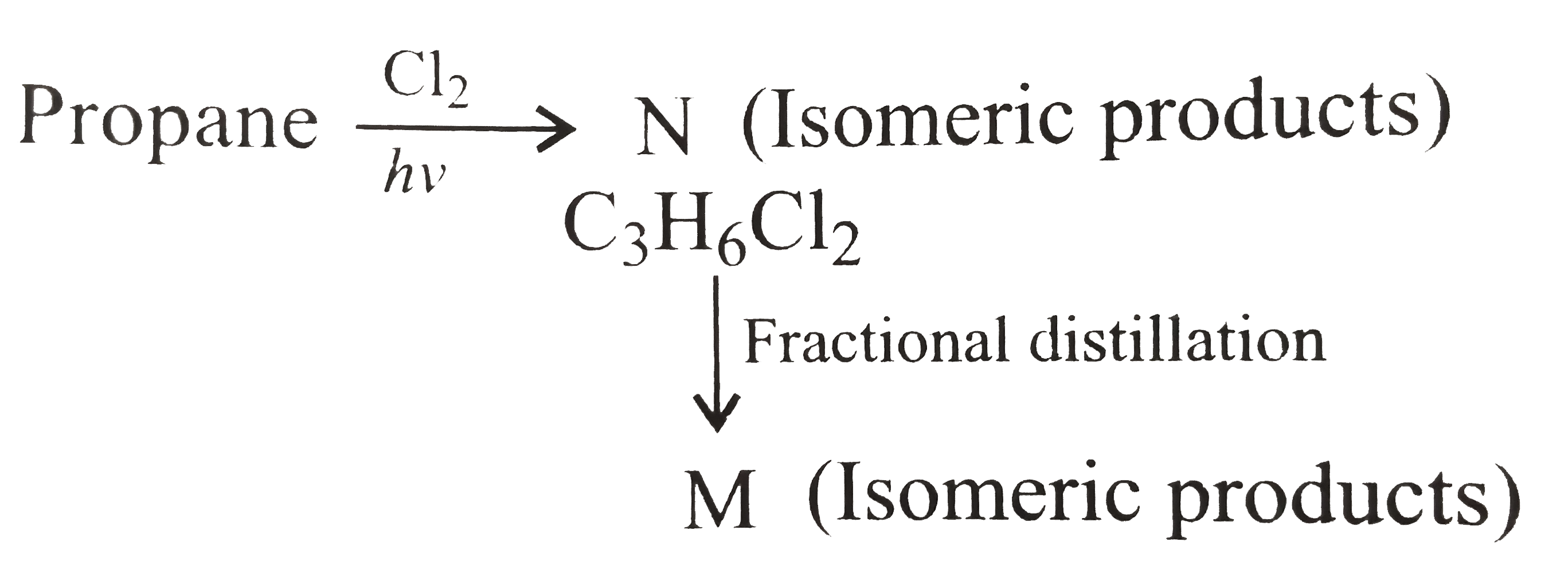
What are the numerical values of N and M?
View Solution
