There are six locks exactly with one key for each lock. All the keys are mixed to each other. The maximum number of attempts needed to get the correct combination is :
21
15
6
can't be determined
The correct Answer is:B
Step by step video, text & image solution for There are six locks exactly with one key for each lock. All the keys are mixed to each other. The maximum number of attempts needed to get the correct combination is : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
There are n locks and n matching keys. If all the locks and keys are to be perfectly matched, find the maximum number of trails required to open a lock.
View SolutionA number lock has 4 dials, each dial has the digits 0, 1, 2,...., .. What is the maximum unsuccessful attempts to open the lock?
View Solution
Knowledge Check
There are six locks exactly with one key for each lock. All the keys are mixed to each other. The maximum number of attempts needed to get the correct combination is :
A21B15C6Dcan't be determinedTintin unlocks the chest, and plugs the key into the main door. A dial emerges on the door. Beginning with the dial set at zero, the dial must be turned counter-clockwise to the first combination number, (then clockwise back to zero), and clockwise to the second combina- tion number, (then counter-clockwise back to zero), and counter-clockwise again to the third and final number, where upon the door shall immediately spring open. There are 40 numbers on the dial, including the zero. Without knowing the combination numbers, what is the maximum number of trials required to open the safe (one trial equals one attempt to dial a full three-number combination)?
A64000B1600C63999D1599In a 'multiple choice question' test there are eight questions. Each question has four alternative of which only one is correct. IF a candidate answers all the questions by choosing one answer for each question, then the number of ways to get exactly 4 correct answer is
A70B2835C5670Dnone of these
There are 2 locks on the door and the keys are among the six different ones you carry in your pocket. In a hurry you dropped one somewhere.The probability that you can still open the door is
View SolutionThe lock of a safe has a dial with holes, sasy ten, in which the numbers 0,1,2,……..9 are inscribed in each hole. The lock can be opened only when a specific code numbersay of six digits is dialled. Suppose the code number is 249916, it means that the can be opened when we first dial 2, then 4 nd so on. Find the maximum number of trials which do not result in opening the lock.
View SolutionA safe is locked by a device consisting of five disks with the digits 0,1,......9 on each of them.The safe gets unlocked by dialing a certain combination of digits. Will ten days be enough to open the safe if the "working day" lasts 13 hours and it takes five seconds to dial one by combination of digits?
View SolutionSix circles each of unit radius are being circumscribed by another larger circle. All the smaller circles touch each other . What is the circumference of the larger circle ?
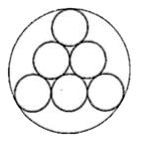
View SolutionThe chest is locked by a number of padlocks. All padlocks must be unlocked in order to open the chest. 12 Copies of the keys to the padlocks are distributed lie next to it, such that any group of 7 or more keys can open the chest should they choose to do so, but any group of less than 7 cannot. What is the minimal number of padlocks required to achieve this?
View Solution
