Question

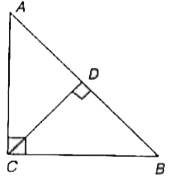
ABC is a right angle triangle at A and AD is perpendicular to the hypotenuse. Then $\frac{BD}{CD}$ is equal to :

Options

A. `((AB)/(AC))^2`
B. `((AB)/(AD))^2`
C. `(AB)/(AC)`
D. `(AB)/(AD)`

Answer

A

Explanation

To solve the problem, we need to find the ratio $$\frac{BD}{CD}$$ in the right triangle $$ABC$$ where $$A$$ is the right angle and $$AD$$ is perpendicular to the hypotenuse $$BC$$.

1. Identify the Triangle and Points:
- We have a right triangle \( ABC \) with \( \angle A = 90^\circ \).
- Point \( D \) is the foot of the perpendicular from \( A \) to the hypotenuse \( BC \).

2. Use the Property of Right Triangles:
- In a right triangle, the segments created by the altitude from the right angle to the hypotenuse have a special relationship. Specifically, we can use the following relationships:
\( \frac{BD}{CD} = \frac{AB^2}{AC^2} \)

3. Set Up the Ratios:
- Let \( AB = c \), \( AC = b \), and \( BC = a \) (the hypotenuse).
- According to the property mentioned, we can express \( BD \) and \( CD \) in terms of the sides of the triangle:
\( BD = \frac{AB^2}{BC} = \frac{c^2}{a} \)
\( CD = \frac{AC^2}{BC} = \frac{b^2}{a} \)

4. Calculate the Ratio:
- Now, substituting these values into the ratio \( \frac{BD}{CD} \):
\( \frac{BD}{CD} = \frac{\frac{c^2}{a}}{\frac{b^2}{a}} = \frac{c^2}{b^2} \)

5. Final Result:
- Therefore, the ratio \( \frac{BD}{CD} \) simplifies to:
\( \frac{BD}{CD} = \left(\frac{AB}{AC}\right)^2 \)
- This means that \( \frac{BD}{CD} \) is equal to the square of the ratio of the lengths of the sides \( AB \) and \( AC \).

Conclusion:
Thus, the answer to the question \( \frac{BD}{CD} \) is \( \frac{AB^2}{AC^2} \).

---