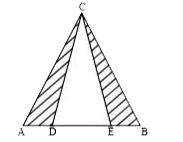
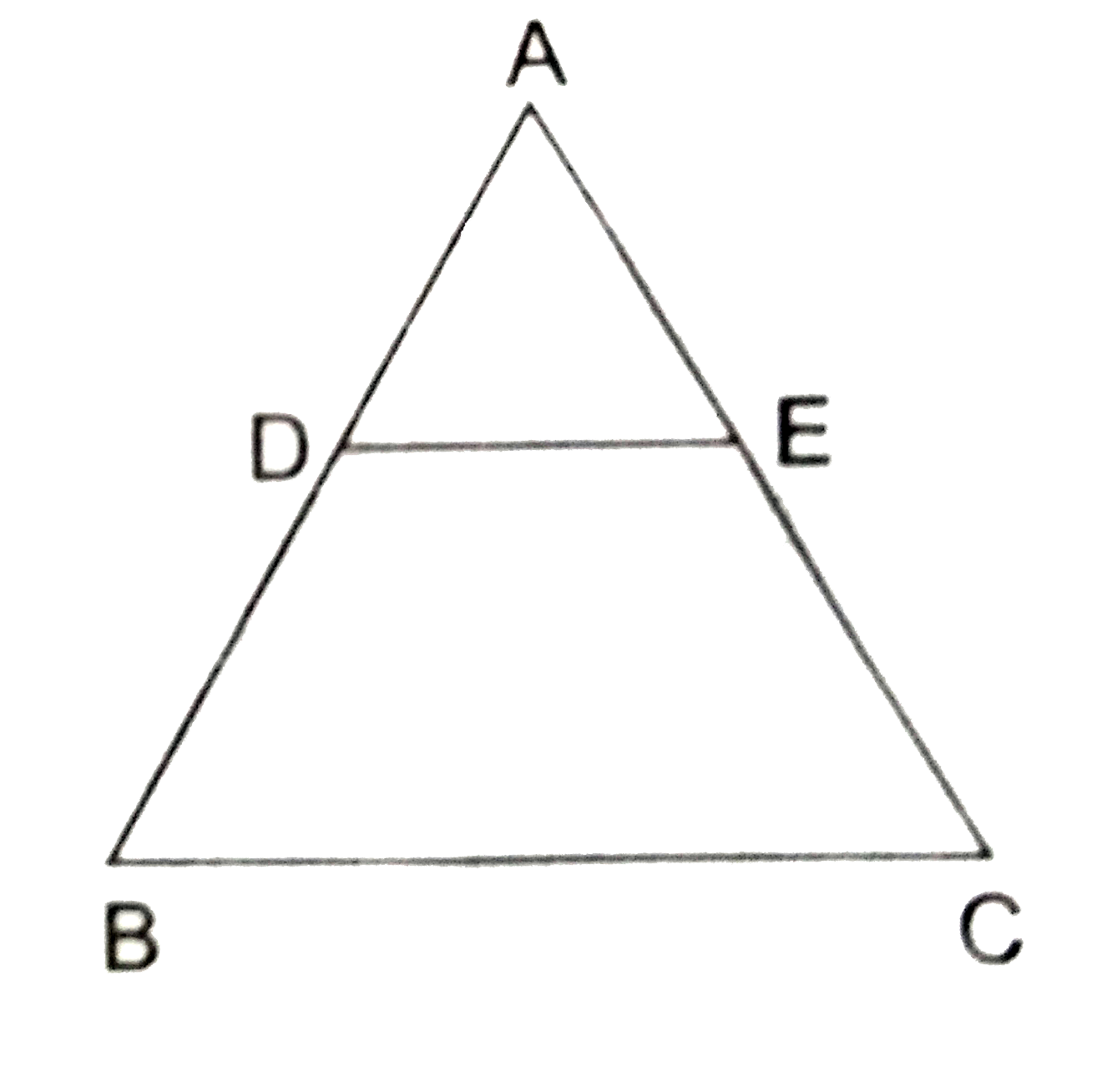
In the equilateral triangle ABC, AD = DE = BE, D and E lies on the AB. If each side of the triangle (i.e., AB, BC and AC) be 6 cm, then the area of the shaded region is:
9cm∘
6√3cm2
5√3cm2
none of the above
The correct Answer is:B
Step by step video solution for In the equilateral triangle ABC, AD = DE = BE, D and E lies on the AB. If each side of the triangle (i.e., AB, BC and AC) be 6 cm, then the area of the shaded region is: by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ΔABC is equilateral triangle. Where AD = DE = BE, D and E lies on the AB. If each side of the triangle be 6cm. Then the area of shaded region.
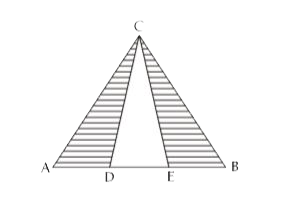
View SolutionIn the equilateral triangle ABC, AD=DE=BE, D and E lie on the AB. If each side of the △ABC is 6cm ,then the area of the shaded region is
View Solution
Knowledge Check
Given an equilateral triangle ABC, D, E and F are the mid-points of the sides AB, BC and AC respectively, then the quadrilateral BEFD is exactly a
AsquareBrectangleCparallelogramDrhombusA straight line parallel to the base BC of the triangle ABC intersects AB and AC at the points D and E respectively. If the area of the ΔABE be 36 sq. cm, then the area of the ΔACD is
A18 sq. cmB36 sq. cmC18 cmD36 cmIn a △ABC,AC=BC, Point D lies on BC such that CD=AD=AB. Find ∠ACB.
AA)18∘BB)30∘CC)36∘DD)48∘
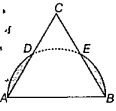
The diameter of a semicircle and the base of an equilateral △ABC coincide in such a way that the other two sides of the triangle intersect the circumference of the semicircle at the points D and E, as shown in the diagram. If the perimeter of the triangle ABC is 6 cm, find the area of the shaded region.
View SolutionABC is a right-angled triangle at A. Semicircles drawn on AB, AC and BC as diameters. Find area of the shaded region.

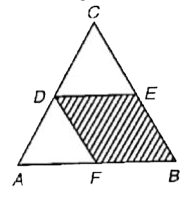
View SolutionABC is a triangle in which D, E and F are the mid-points of the sides AC, BC and AB respectively. What is the ratio of the area of the shaded to the unshaded region in the triangle?
View SolutionIn an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?
View SolutionIn ΔABC, AB=AC and D is a point on side AC such that BD = BC, If AB = 12.5 cm and BC = 5 cm, then what is the measure of DC ?
View Solution
