A circle with radius 12 cm has two perpendicular chords AB and CD intersecting at a point R, other than the centre O, where RD=6cm and RB=18cm. Find the length of AR.
A)6√35
B)4√35
C)4√5
D)data insufficient
The correct Answer is:A
To solve the problem step by step, we will use the information provided about the circle and the chords.
Step 1: Understand the given information
We have a circle with a radius of 12 cm. The two perpendicular chords AB and CD intersect at point R. The lengths given are:
- RD = 6 cm
- RB = 18 cm
We need to find the length of AR, which we will denote as x.
Step 2: Determine the lengths of the segments
Since the chords intersect at R, we can express the lengths of the segments:
- Let AR = x
- Since RB = 18 cm, we have RB=18
- Let CR = y
Step 3: Use the property of perpendicular chords
In a circle, if two chords intersect, the products of the lengths of the segments of each chord are equal. Therefore, we can write:
AR⋅RB=CR⋅RD
Substituting the known values:
x⋅18=y⋅6
From this, we can express y in terms of x:
y=18x6=3x
Step 4: Apply the Pythagorean theorem
Since the chords are perpendicular, we can use the Pythagorean theorem. The relationship between the segments and the radius of the circle can be expressed as:
AR2+RB2+CR2+RD2=Diameter2
The diameter of the circle is 2×radius=24 cm, so:
242=576
Substituting the values we have:
x2+182+(3x)2+62=576
Calculating the squares:
x2+324+9x2+36=576
Combining like terms:
10x2+360=576
Step 5: Solve for x2
Subtract 360 from both sides:
10x2=576−360
10x2=216
Now, divide by 10:
x2=21610=1085
Step 6: Find the value of x
Taking the square root:
x=√1085=√108√5=6√3√5
Step 7: Final answer
Thus, the length of AR is:
AR=6√3√5 cm
We have a circle with a radius of 12 cm. The two perpendicular chords AB and CD intersect at point R. The lengths given are:
- RD = 6 cm
- RB = 18 cm
Since the chords intersect at R, we can express the lengths of the segments:
- Let AR = x
- Since RB = 18 cm, we have RB=18
- Let CR = y
In a circle, if two chords intersect, the products of the lengths of the segments of each chord are equal. Therefore, we can write:
AR⋅RB=CR⋅RD
Substituting the known values:
x⋅18=y⋅6
From this, we can express y in terms of x:
y=18x6=3x
Since the chords are perpendicular, we can use the Pythagorean theorem. The relationship between the segments and the radius of the circle can be expressed as:
AR2+RB2+CR2+RD2=Diameter2
The diameter of the circle is 2×radius=24 cm, so:
242=576
Substituting the values we have:
x2+182+(3x)2+62=576
Calculating the squares:
x2+324+9x2+36=576
Combining like terms:
10x2+360=576
Subtract 360 from both sides:
10x2=576−360
10x2=216
Now, divide by 10:
x2=21610=1085
Taking the square root:
x=√1085=√108√5=6√3√5
Thus, the length of AR is:
AR=6√3√5 cm
Topper's Solved these Questions
Similar Questions
In a circle, chords AB and CD intersect at a point R inside the circle. If AR : RB = 1:4 and CR: RD = 4:9, then the ratio AB: CD is
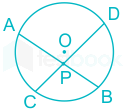
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point p within the circle. If AB=15cm,PB=9cm, then find the length of PD.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
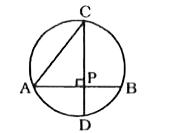
Two mutually perpendicular chords AB and CD intersect at point P inside the circle such that CP=15cm.,PD=8cmandPB=6cm. Find the length AC (in cm.)
 A25B24C20D18
A25B24C20D18 - Question 2 - Select One
The two chords AB and CD of a circle intersect at point P, such that BP=4 cm, PD=5 cm, and CP=8 cm. find the length of chord AB.
A8B10C12D14 - Question 3 - Select One
Chords AB and CD of a circle intersect externally at P. If AB=6cm,CD=3cmandPD=5cm, then the length of PB is
A5 cmB7.35 cmC6 cmD4 cm
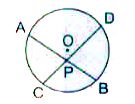
In the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point P within the circle. If AB = 18 cm, PB = 8 cm, CP = 5 cm, then find the length of CD.
 View Solution
View SolutionTwo circles of radii 5 cm and 3cm intersect at two points and the distance between their centres is 4cm. Find the length of the common chord.
Let the common chord be AB and Pand Q be the centers of the two circles.
AP=5cmand AQ=3cm.
PQ=4cm ...given
Now, segPQ⊥chordAB
AR=RB=12AB....perpendicular from center to the chord, bisects the chord
Let PR=xcm
so RQ=(4−x)cm
In△ARP,AP2=AR2+PR2
AR2=52−x2...(1)
In △ARQ,AQ2=AR2+QR2
AR2=32−(4−x)2...(2)
52−x2=32−(4−x)2...from (1) & (2)
25−x2=9−(16−8x+x2)
25−x2=−7+8x−x2
32=8x
x=4 substituting in equation(1) we get , AR2=25−16=9
AR=3cm
AB=2×AR=2×3=6
AB=6cmSo length of common chord is6 cm.View SolutionTwo circles of radil 5cm and 3cm intersect at two points and the distance between their centres is 4cm. Find the length of the common chord.
View SolutionTwo circles of radii 5 cm and 3 cm intersect at two distinct points. Their centres are 4 cm apart. Find the length of their common chord.
View SolutionThere is a circle of radius 5 cm. There are two chords AB and AC OF equal length = 6 cm . Find the length of chord BC .
View Solution

