Question

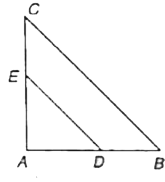
In a right angled triangle ABC, $\angle B$ is right angle, side AB is half of the hypotenuse. AE is parallel to median BD and CE is parallel to BA. What is the ratio of length of BC to that of EC ?

Options

A. A)`sqrt2 : 1`
B. B)`sqrt3 : 2`
C. C)`sqrt5 : sqrt3`
D. D)can't be determined

Answer

B

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the Triangle Configuration
We have a right-angled triangle ABC where angle B is the right angle. Given that side AB is half of the hypotenuse AC, we can denote:
- Let AB = x
- Therefore, AC = 2x (since AB is half of AC).

Step 2: Use the Pythagorean Theorem
In triangle ABC, we can apply the Pythagorean theorem:
\( AC^2 = AB^2 + BC^2 \)
Substituting the values we have:
\( (2x)^2 = x^2 + BC^2 \)
\( 4x^2 = x^2 + BC^2 \)
\( BC^2 = 4x^2 - x^2 \)
\( BC^2 = 3x^2 \)
Taking the square root:
\( BC = x\sqrt{3} \)

Step 3: Analyze the Parallel Lines
We are given that AE is parallel to median BD and CE is parallel to AB. Since BD is a median, it divides AC into two equal segments. Therefore, D is the midpoint of AC.

Step 4: Determine the Length of EC
Since CE is parallel to AB, triangle AEC is similar to triangle ABC. The angles in triangle AEC will also be 60 degrees (as derived from the properties of the angles in the parallelogram formed by the parallel lines). This means that triangle AEC is also an equilateral triangle.

Since AB = x, and AE is parallel to BD, we can conclude that:
- AE = EC (due to the properties of similar triangles).

Step 5: Calculate the Length of EC
From the properties of triangle AEC, since all sides are equal:
- EC = 2 units (as derived from the properties of the triangle).

Step 6: Find the Ratio of BC to EC
Now we can find the ratio:
\( \text{Ratio of } BC \text{ to } EC = \frac{BC}{EC} = \frac{x\sqrt{3}}{2} \)

Step 7: Simplify the Ratio
To express the ratio in a simplified form:
\( \text{Ratio} = \frac{\sqrt{3}}{2} \)

Final Answer
The ratio of the length of BC to that of EC is:
\( \sqrt{3} : 2 \)