There are two congruent triangles each with area 198cm2?. Triangle DEF is placed over triangle ABC in such a way that the centroid of both the triangles coincides with each other and AB∣∣DE, as shown in figure, thus forming a star. What is the area of the common region (PQRSTU)?

99cm2
132cm2
148cm2
can't be determined
The correct Answer is:B
Step by step video & image solution for There are two congruent triangles each with area 198 cm^(2)?. Triangle DEF is placed over triangle ABC in such a way that the centroid of both the triangles coincides with each other and AB || DE, as shown in figure, thus forming a star. What is the area of the common region (PQRSTU)? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Triangle ABC is such that AB=9cm,BC=6cm,AC=7.5cm. Triangle DEF is similar to ΔABC. If EF = 12 cm then DE is :
A6 cmB16 cmC18 cmD15 cmIn the figure , triangle ABC is isosceles in which AB = AC = 6 cm . If the radius of circle is 9 cm then what is the area of the triangle?
A8√2cm2B8cm2C2√2cm2D8√2cm2Triangle ABC and DEF are similar. If AC = 19 cm and DF = 8 cm , the ratio of the area of two triangles are :
A198B36164C3865DNone of these
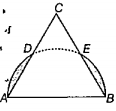
The diameter of a semicircle and the base of an equilateral △ABC coincide in such a way that the other two sides of the triangle intersect the circumference of the semicircle at the points D and E, as shown in the diagram. If the perimeter of the triangle ABC is 6 cm, find the area of the shaded region.
View SolutionThe areas of two similar triangles ABC and DEF are 144cm2and81cm2 respectively . If the longest side of the larger triangle is 36 cm , find the longest side of the other triangle .
View SolutionThe area of triangle ABC = 30.1cm2. calculate the height of triangle ABD,If AB = 4.3cm.
View SolutionEach of sides of a triangle is 8 cm less than the sum of its other two sides. Area of the triangle (in cm2) is
View SolutionIf each sides of a triangle is doubled then find the ratio of the area of the new triangle thus formed and the given triangle.
View Solution