In a group of 132 people 50, 60, 70 people like three different sweets-Barfi, Jalebi, Rasgulla, respectively. The number of people who like all the three sweets is half the number of people who like exactly two sweets. The number of people who like exactly any two out of the three sweets is the same as those who like exactly any other two of the three sweets. find the number of people who like Rasgulla or Jalebi but not Barfi
82
42
48
38
The correct Answer is:A
To solve the problem step by step, we will use the information provided and set up equations based on the given conditions.
Step 1: Define Variables
Let:
- B = Number of people who like Barfi = 50
- J = Number of people who like Jalebi = 60
- R = Number of people who like Rasgulla = 70
- G = Number of people who like all three sweets
- D = Number of people who like both Barfi and Jalebi (but not Rasgulla)
- F = Number of people who like both Barfi and Rasgulla (but not Jalebi)
- E = Number of people who like both Jalebi and Rasgulla (but not Barfi)
Step 2: Set Up Equations
From the problem statement, we know:
1. The total number of people is 132.
2. The number of people who like all three sweets is half the number of people who like exactly two sweets:
G=12(D+E+F)
3. The number of people who like exactly any two out of the three sweets is the same:
D=E=F
Let D=E=F=x.
Step 3: Substitute and Simplify
Substituting D,E,F with x:
- The equation for G becomes:
G=12(x+x+x)=3x2
Step 4: Write Total Equations for Each Sweet
Using the total counts for each sweet:
1. For Barfi:
B=D+F+G+(only Barfi)⟹50=x+x+3x2+(only Barfi)
This simplifies to:
50=2x+3x2+(only Barfi)⟹50=7x2+(only Barfi)
2. For Jalebi:
J=D+E+G+(only Jalebi)⟹60=x+x+3x2+(only Jalebi)
This simplifies to:
60=2x+3x2+(only Jalebi)⟹60=7x2+(only Jalebi)
3. For Rasgulla:
R=F+E+G+(only Rasgulla)⟹70=x+x+3x2+(only Rasgulla)
This simplifies to:
70=2x+3x2+(only Rasgulla)⟹70=7x2+(only Rasgulla)
Step 5: Solve for x
Now, we can express the total number of people in terms of x:
(only Barfi)+(only Jalebi)+(only Rasgulla)+D+E+F+G=132
Substituting the values:
(only Barfi)+(only Jalebi)+(only Rasgulla)+3x+3x2=132
Step 6: Solve the Equations
From the equations for Barfi, Jalebi, and Rasgulla, we can find the number of people who only like each sweet.
1. From Barfi:
(only Barfi)=50−2x−3x2=50−7x2
2. From Jalebi:
(only Jalebi)=60−2x−3x2=60−7x2
3. From Rasgulla:
(only Rasgulla)=70−2x−3x2=70−7x2
Step 7: Substitute Back and Solve
Now we can substitute these back into the total equation and solve for x:
(50−7x2)+(60−7x2)+(70−7x2)+3x+3x2=132
Combine like terms and solve for x.
Step 8: Calculate the Values
After solving, we find:
- x=8
- G=12
- D=E=F=8
- Calculate the number of people who like Rasgulla or Jalebi but not Barfi:
E+R=8+42=50
Final Answer
The number of people who like Rasgulla or Jalebi but not Barfi is 82.
Let:
- B = Number of people who like Barfi = 50
- J = Number of people who like Jalebi = 60
- R = Number of people who like Rasgulla = 70
- G = Number of people who like all three sweets
- D = Number of people who like both Barfi and Jalebi (but not Rasgulla)
- F = Number of people who like both Barfi and Rasgulla (but not Jalebi)
- E = Number of people who like both Jalebi and Rasgulla (but not Barfi)
From the problem statement, we know:
1. The total number of people is 132.
2. The number of people who like all three sweets is half the number of people who like exactly two sweets:
G=12(D+E+F)
3. The number of people who like exactly any two out of the three sweets is the same:
D=E=F
Let D=E=F=x.
Substituting D,E,F with x:
- The equation for G becomes:
G=12(x+x+x)=3x2
Using the total counts for each sweet:
1. For Barfi:
B=D+F+G+(only Barfi)⟹50=x+x+3x2+(only Barfi)
This simplifies to:
50=2x+3x2+(only Barfi)⟹50=7x2+(only Barfi)
J=D+E+G+(only Jalebi)⟹60=x+x+3x2+(only Jalebi)
This simplifies to:
60=2x+3x2+(only Jalebi)⟹60=7x2+(only Jalebi)
R=F+E+G+(only Rasgulla)⟹70=x+x+3x2+(only Rasgulla)
This simplifies to:
70=2x+3x2+(only Rasgulla)⟹70=7x2+(only Rasgulla)
Now, we can express the total number of people in terms of x:
(only Barfi)+(only Jalebi)+(only Rasgulla)+D+E+F+G=132
Substituting the values:
(only Barfi)+(only Jalebi)+(only Rasgulla)+3x+3x2=132
From the equations for Barfi, Jalebi, and Rasgulla, we can find the number of people who only like each sweet.
(only Barfi)=50−2x−3x2=50−7x2
2. From Jalebi:
(only Jalebi)=60−2x−3x2=60−7x2
3. From Rasgulla:
(only Rasgulla)=70−2x−3x2=70−7x2
Now we can substitute these back into the total equation and solve for x:
(50−7x2)+(60−7x2)+(70−7x2)+3x+3x2=132
Combine like terms and solve for x.
After solving, we find:
- x=8
- G=12
- D=E=F=8
- Calculate the number of people who like Rasgulla or Jalebi but not Barfi:
E+R=8+42=50
The number of people who like Rasgulla or Jalebi but not Barfi is 82.
Topper's Solved these Questions
Similar Questions
In a group of 132 people 50, 60, 70 people like three different sweets-Barfi, Jalebi, Rasgulla, respectively. The number of people who like all the three sweets is half the number of people who like exactly two sweets. The number of people who like exactly any two out of the three sweets is the same as those who like exactly any other two of the three sweets. find the number of people who like Rasgulla or Jalebi but not Barfi
View SolutionFind out the number of people who do not play any game.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In a group of 132 people 50, 60, 70 people like three different sweets-Barfi, Jalebi, Rasgulla, respectively. The number of people who like all the three sweets is half the number of people who like exactly two sweets. The number of people who like exactly any two out of the three sweets is the same as those who like exactly any other two of the three sweets. The number of people who like the three sweets
A12B6C8Dnone of these - Question 2 - Select One
In a group of 132 people 50, 60, 70 people like three different sweets-Barfi, Jalebi, Rasgulla, respectively. The number of people who like all the three sweets is half the number of people who like exactly two sweets. The number of people who like exactly any two out of the three sweets is the same as those who like exactly any other two of the three sweets. The number of people who like the three sweets
A12B6C8Dnone of these - Question 3 - Select One
In a group of 132 people 50, 60, 70 people like three different sweets-Barfi, Jalebi, Rasgulla, respectively. The number of people who like all the three sweets is half the number of people who like exactly two sweets. The number of people who like exactly any two out of the three sweets is the same as those who like exactly any other two of the three sweets. find the number of people who like Rasgulla or Jalebi but not Barfi
A82B42C48D38
The pie chart given below shows the distribution of students who like the given 5 sports. The total number of students is 960.
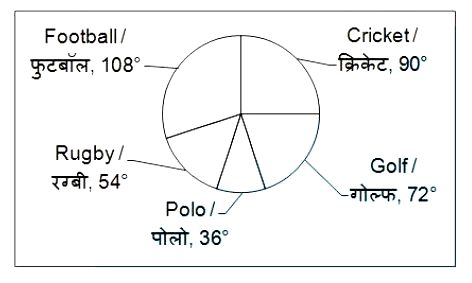
The total number of students who like these 2 sports is equal to the number of students who like Cricket. Which are these 2 sports?View SolutionFrom the details, find out the number of people who do not read any newspaper.
 View Solution
View SolutionIn a group of 132 people 50, 60, 70 people like three different sweets-Barfi, Jalebi, Rasgulla, respectively. The number of people who like all the three sweets is half the number of people who like exactly two sweets. The number of people who like exactly any two out of the three sweets is the same as those who like exactly any other two of the three sweets. The number of people who like the three sweets
View SolutionChildren like to eat sweets, isn't it?
View SolutionWhat is the respective ratio of the number of teachers who teach Mathematics and the number of teach- ers who teach Hindi? ?
 View Solution
View Solution

