If 0<a<1 and 9≤b≤10, then
9≤a+b≤11
9≤a+b<11
9<a+b≤11
9<a+b<11
The correct Answer is:D
Step by step video, text & image solution for If 0ltalt1 and 9leble10, then by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the adjoining diagram graphs of logax and logbx are shown for x>0 and 0<a<1, then :
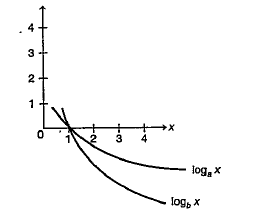 Aa<bBa>bCcan't be determinedDnone of the above
Aa<bBa>bCcan't be determinedDnone of the above - Question 2 - Select One
If A×A has 9 elements two of which are (-1,0) and (0,1) then the set A is
A{−1,0}B{−1,1}C{−1,0,1}D{0,1} - Question 3 - Select One
If 3≤a≤2015,3≤b≤2015 such that logab+6logba=5, the number of ordered pairs (a,b) of integers is
A48B50C52D54
[ Supposea∈R,a≠−12 .Let α,β be roots of (2a+1)x2−ax+a−2=0If α<1<β, then [ (a)17(6−2√23)<a<1(b)17(6−2√23)<a<12(c)12<a<17(6+2√23)( d) none of these ]]
View SolutionIf 0∘<A<90∘, then cosecA−cotA,sinA,cosecA+cotA are in
View SolutionIf a=∫2121xcot7(x−1x)dx, then (A) a=0 (B) 0<a<1 (C) a>0 (D) none of these
View SolutionA function is defined as f(x)=ax∀x∈Rand0<a<1, then which of the following is true?
(i) It is an increasing function
(ii) It is a decreasing function
(iii) All such functions must meet at (0, 1)View SolutionA function is defined as f(x)=ax∀x∈R and 0<a<1, then which of the following is true?
(i) It is an increasing function
(ii) It is a decreasing function
All such functions must meet at (0,1)View Solution
