In the adjoining figure ABC is an equilateral triangle and C is the centre of the circle, A and B lie on the circle. What is the area of the shaded region , if the diameter of the circle is 28 cm ?

(10223−49√3)cm2
(10323−98√3)cm2
(109−38√3)cm
none of the above
The correct Answer is:A
Step by step video & image solution for In the adjoining figure ABC is an equilateral triangle and C is the centre of the circle, A and B lie on the circle. What is the area of the shaded region , if the diameter of the circle is 28 cm ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
Similar Questions
In the figure ABCD is a square,whose vertices lie on the circle.Find the area of the shaded region,if the perimeter of the circle is 88 cm
View SolutionIn the given figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O, then the area of the shaded region is :
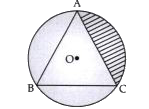 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the adjoining figure ∠AOC=140∘ where is the centre of the circle then ∠ABC is equal to :
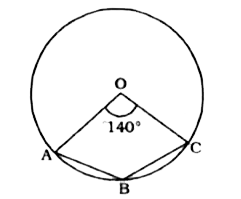 A110∘B100∘C90∘D40∘
A110∘B100∘C90∘D40∘ - Question 2 - Select One
If BC passes through centre of the circle, then the area of the shaded region in the given figure is:
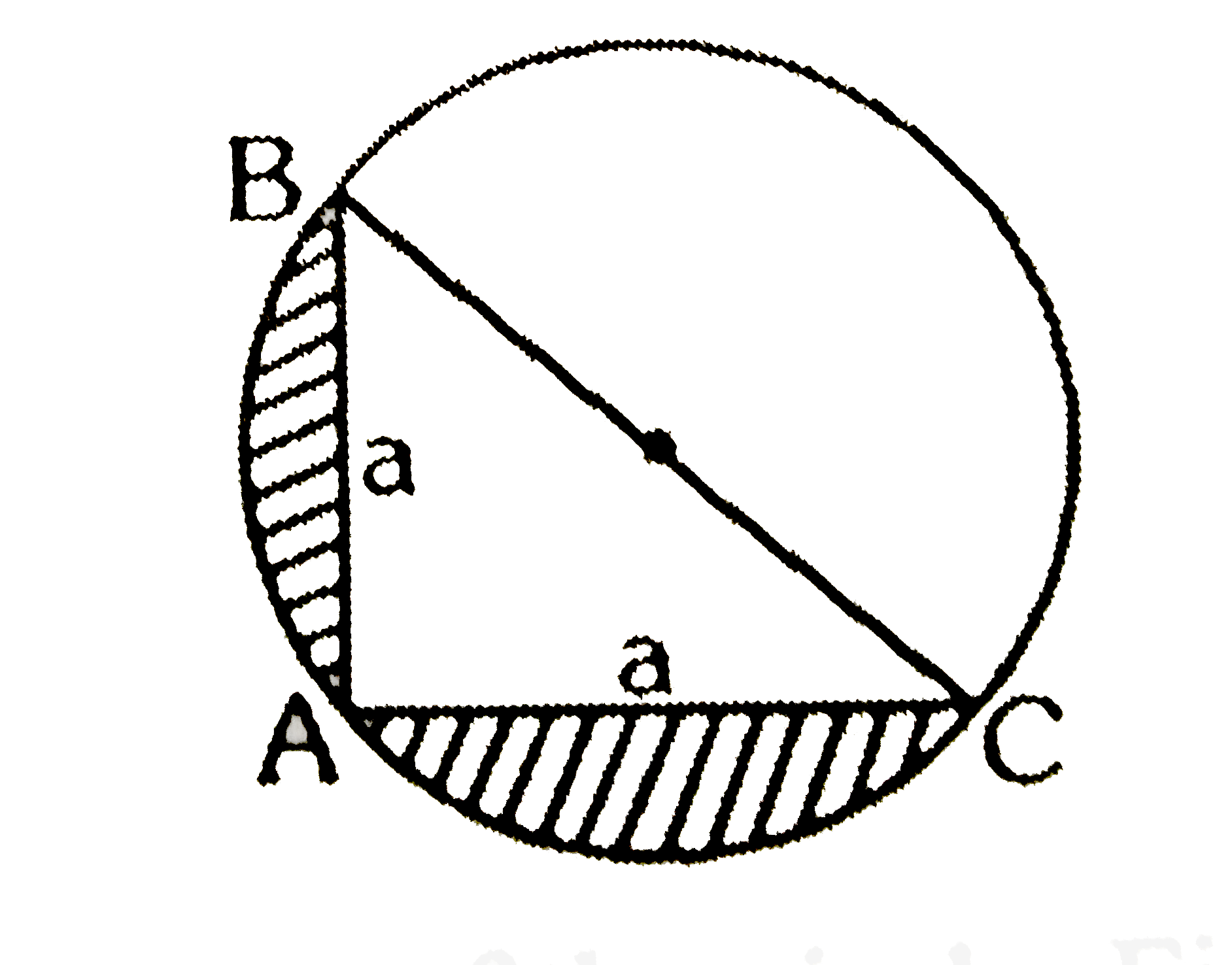 Aa22(3−π)Ba2(π2−1)C2a2(π−1)Da22(π2−1)
Aa22(3−π)Ba2(π2−1)C2a2(π−1)Da22(π2−1)
If the radius of the circle is 6 cm, then the area of the shaded region shown in the figure is
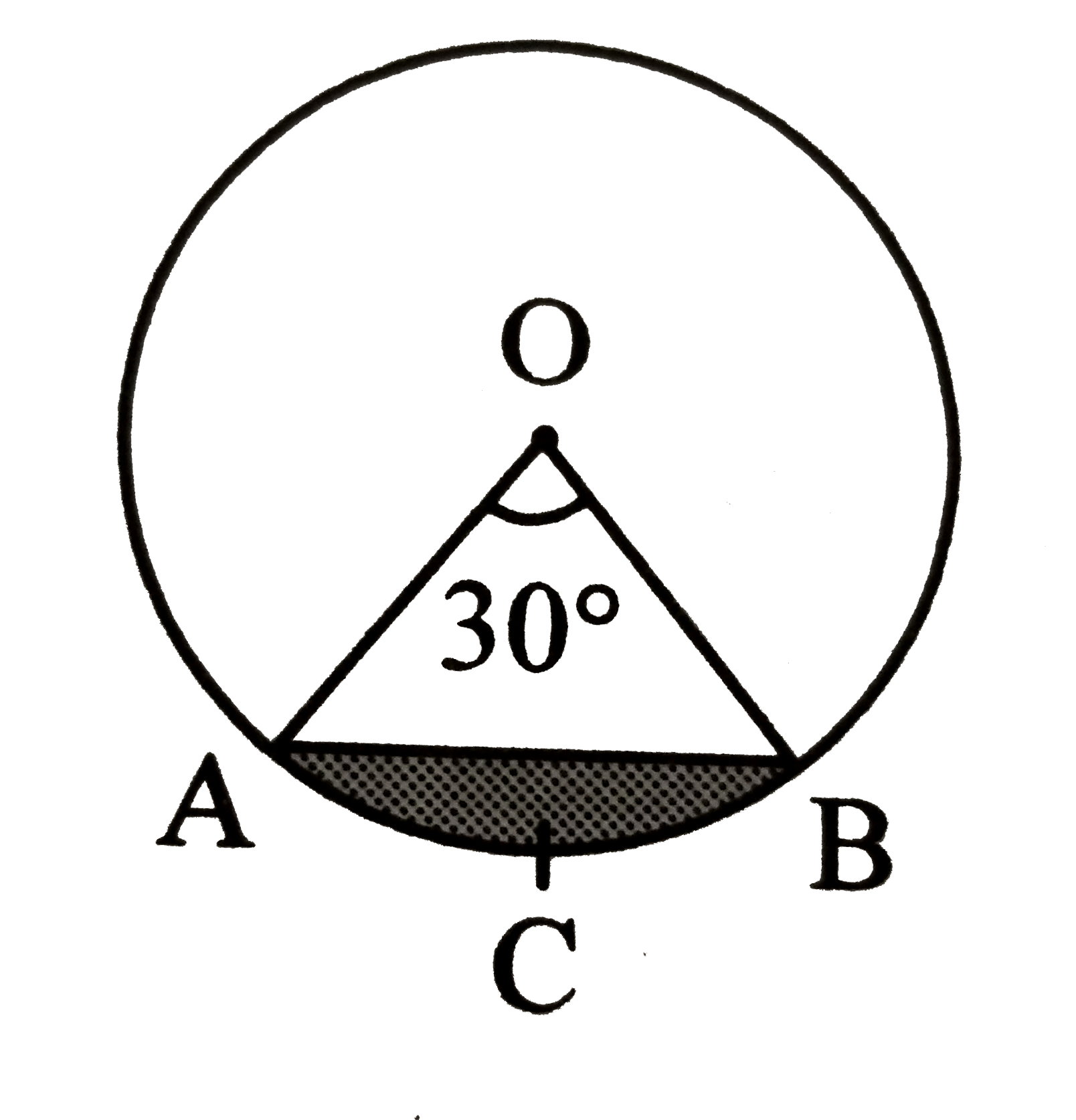 View Solution
View SolutionIn the adjoining figure, PQR is an equilateral triangle inscribed in a circle of radius 7cm. Find the area of the shaded region.
View SolutionIn Fig. 19.60, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O . Find the area of the shaded region. (FIGURE)
View SolutionIn the figure, O is the centre of the circle. ∠POQ=90∘ .
The area of the shaded region is 126cm2. Find the radius of the circle.
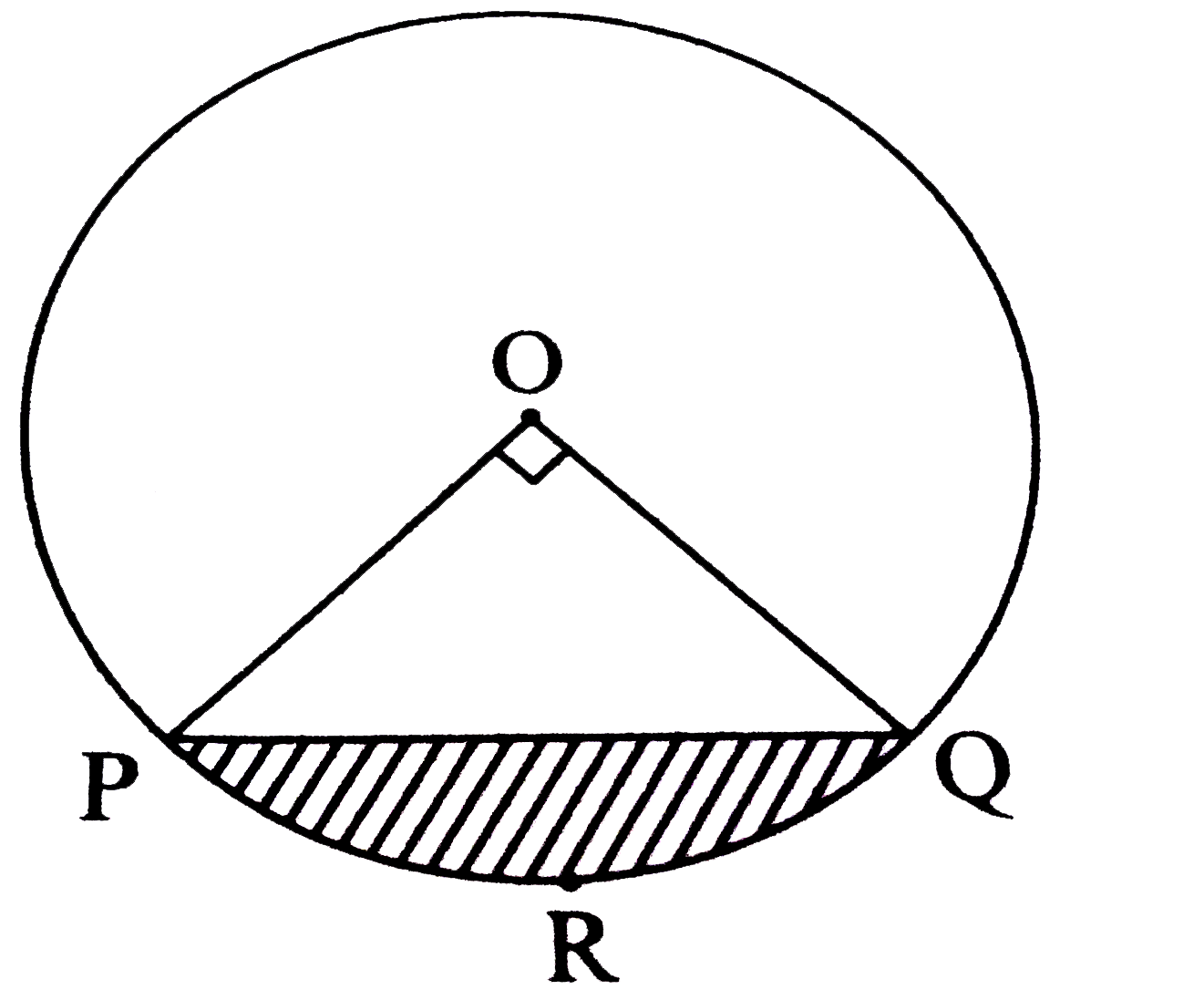 View Solution
View SolutionIn the adjoining figure, CM = 5 cm, RB = 9 cm, CD⊥AB, O is the centre of larger circle and K is the centre of smaller circle. Find the area of shaded region
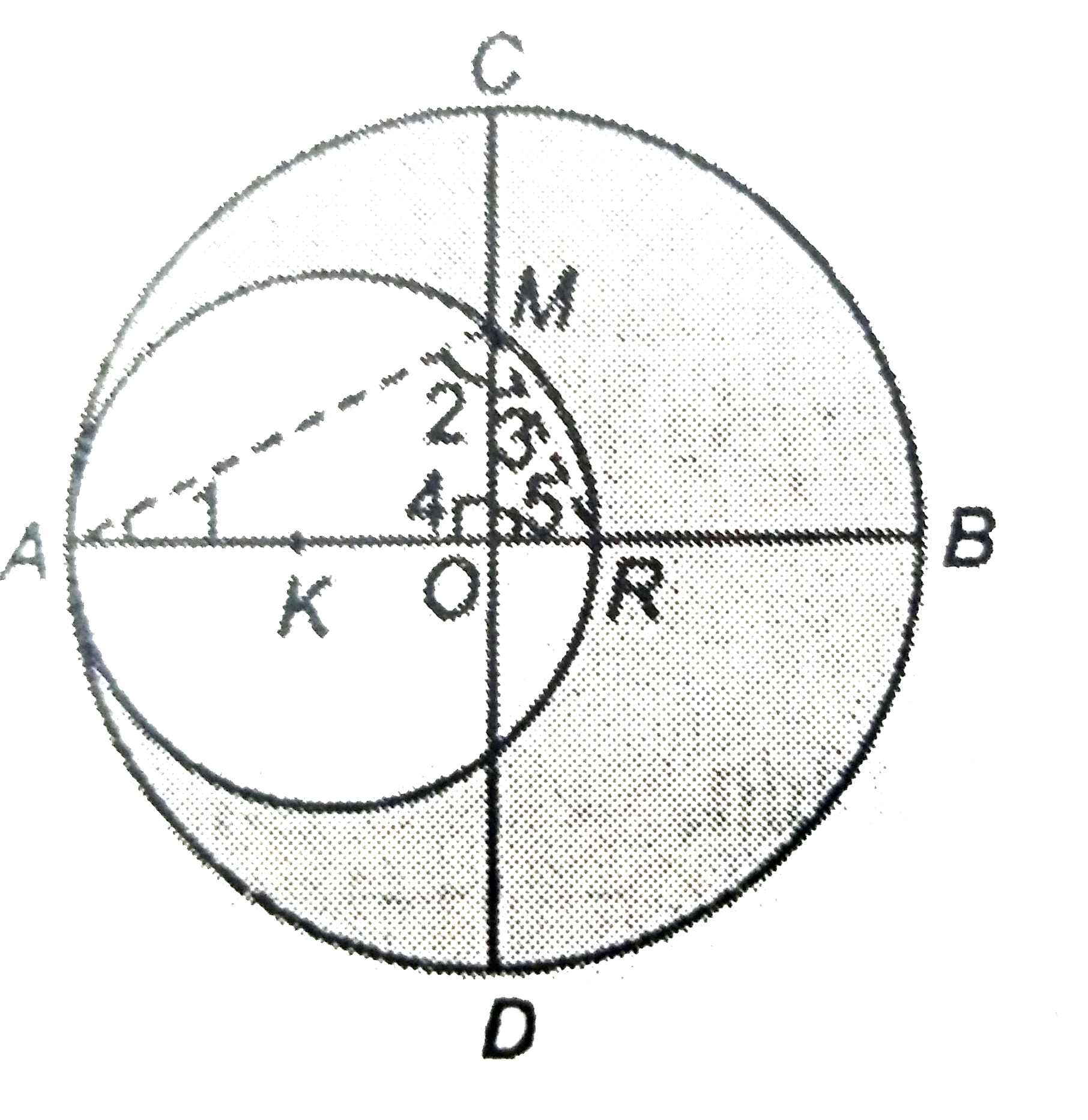 View Solution
View SolutionAn equilateral triangle has one of its side coinciding with the diameter of the unit circle. The area of the region inside the triangle but outside the circle is
View Solution

