An ant has to go from one corner to the farthest corner of a canister of size 6×6×12. What's the minimum diatance it has to cover, (All the lengths are in cm)?
6(√2+2)
6√6
12√2
13(√2+1)
The correct Answer is:C
To find the minimum distance the ant has to cover from one corner of a cuboidal canister to the farthest corner, we can follow these steps:
1. Identify the Dimensions of the Canister:
The canister has dimensions of 6 cm x 6 cm x 12 cm.
2. Label the Corners of the Cuboid:
Let's label the corners of the cuboid:
- A (0, 0, 0) - one corner
- B (6, 0, 0)
- C (6, 6, 0)
- D (0, 6, 0)
- E (0, 0, 12)
- F (6, 0, 12)
- G (6, 6, 12)
- H (0, 6, 12)
The ant starts at corner A and needs to reach corner F.
3. Determine the Path:
The ant can take the following path:
- From A to C (moving along the base)
- From C to F (moving vertically)
4. Calculate the Distance AC:
The distance AC can be calculated using the Pythagorean theorem:
AC=√(AB)2+(BC)2
Here, AB = 6 cm and BC = 6 cm.
AC=√(6)2+(6)2=√36+36=√72=6√2 cm
5. Calculate the Distance CF:
The distance CF is simply the height of the canister:
CF=12 cm
6. Total Distance:
The total distance the ant needs to cover from A to F is:
Total Distance=AC+CF=6√2+12 cm
7. Final Expression:
We can factor out the common terms:
Total Distance=6√2+12=6(√2+2) cm
Conclusion:
The minimum distance the ant has to cover is 6(√2+2) cm.
The canister has dimensions of 6 cm x 6 cm x 12 cm.
Let's label the corners of the cuboid:
- A (0, 0, 0) - one corner
- B (6, 0, 0)
- C (6, 6, 0)
- D (0, 6, 0)
- E (0, 0, 12)
- F (6, 0, 12)
- G (6, 6, 12)
- H (0, 6, 12)
The ant starts at corner A and needs to reach corner F.
The ant can take the following path:
- From A to C (moving along the base)
- From C to F (moving vertically)
The distance AC can be calculated using the Pythagorean theorem:
AC=√(AB)2+(BC)2
Here, AB = 6 cm and BC = 6 cm.
AC=√(6)2+(6)2=√36+36=√72=6√2 cm
The distance CF is simply the height of the canister:
CF=12 cm
The total distance the ant needs to cover from A to F is:
Total Distance=AC+CF=6√2+12 cm
We can factor out the common terms:
Total Distance=6√2+12=6(√2+2) cm
The minimum distance the ant has to cover is 6(√2+2) cm.
Topper's Solved these Questions
Similar Questions
An insect moves with a constant velocity v from one corner of a room to other corner which is opposite of the first corner along the largest diagonal of room.If the insect can not fly and dimensions of a room is a x a x a then the minimum time in which the insect can move is a/v times the square root of a number n then n is equal to?
View SolutionA room has dimensions 3m×4m×5m. A fly starting at one corner ends up at the diametrocally opposite corner .
(a). What is the magnetic of its displacement ?
(b) Could the length of its path be less than this distance ?
(c) Choosing a situtable cooridinate system find the position vector .
(d) If the fly does not fly but walks , what is the lenght of the shortest path it can take ?View Solution
Knowledge Check
- Question 1 - Select One
A cubical room has dimensions 4ft×4ft×4ft . An insect starts from one corner O and reaches a corner on the opposite side of the body diagonal.
Suppose that insect does not fly but crawls. Find the minimum distance travelled by insect to reach the destination.A(4√s+4)ftB√48ftC√80ftDNone of these - Question 2 - Select One
An elephant of length 4 m is at one corner of a rectangular cage of side (16m×30m) and faces towards the diagonally opposite corner. If the elephant starts moving towards the diagonally opposite corner it takes 15 seconds to reach this corner. Find the speed of the elephant.
A1m/secB2m/secC1.87 m/secD1.5 m/sec - Question 3 - Select One
Cosider a regular cube with positive point charge + Q in all corners except for one which has a negative point chnarge -Q .Let the distance from any corner to the centre of the cube be r. what is the magitude of elelctric fleld at point P the centre of the cude ? (K=14πε0)
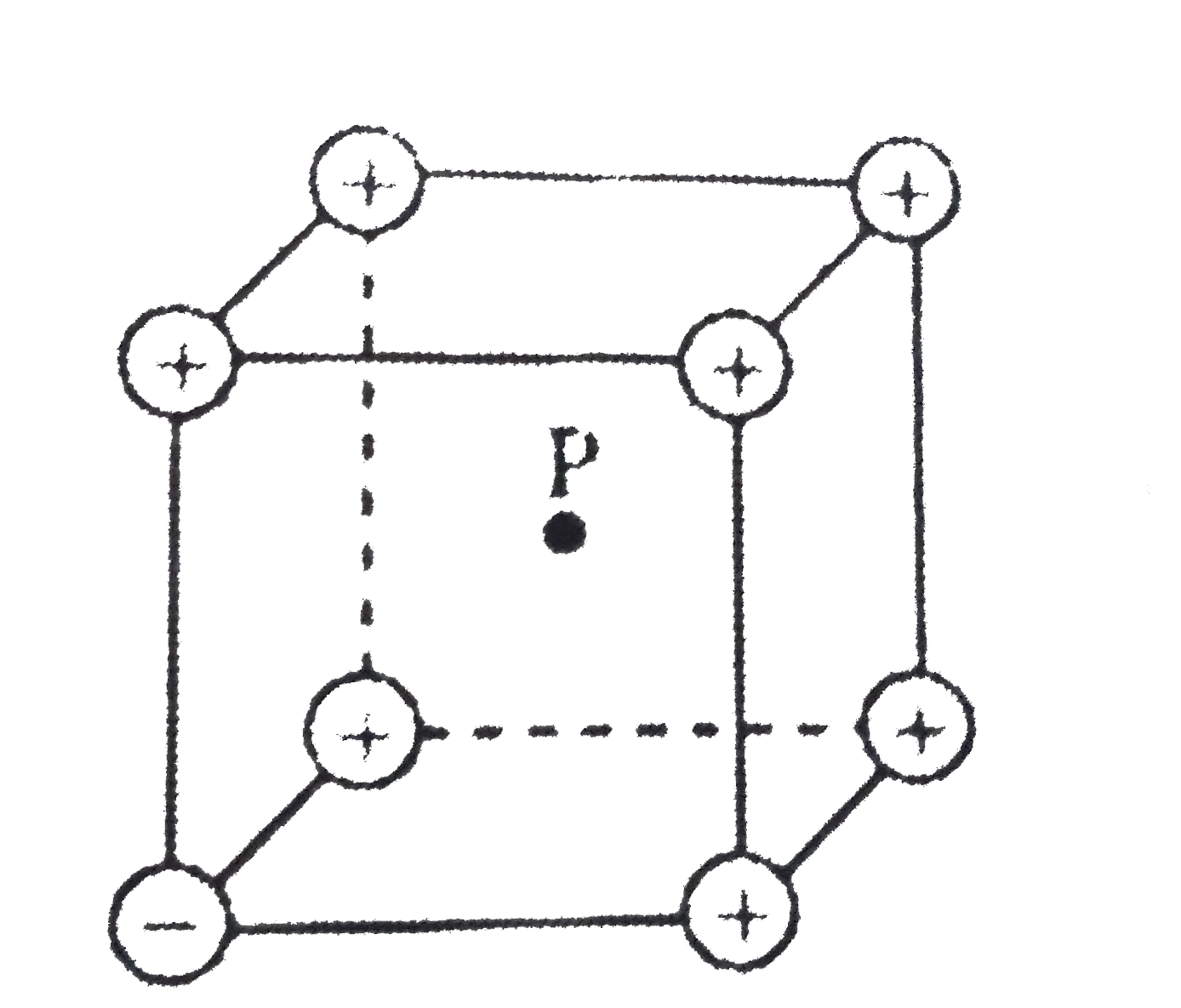 AE=7KQ/r2BE=KQ/r2CE=2KQ/r2DE=6KQ/r2
AE=7KQ/r2BE=KQ/r2CE=2KQ/r2DE=6KQ/r2
In the figure below, a circle is inscribed inside a square. In the gap between the circle and the square (at the corner) a rectangle measuring 20 cm. × 10 cm. is drawn such that the corner A of the rectangle is also a point on the circumference of the circle. What is the radius of the circle in cm?
 View Solution
View SolutionA cubical room has dimensions 4ft×4ft×4ft . An insect starts from one corner O and reaches a corner on the opposite side of the body diagonal.
In previous problem, the magnitude of displacement is :View SolutionA black ant has to go from the origin to a point (6, 4) on the Cartesian plane, using the coordinate axes. However, it avoids crossing the point (4, 1), as a red ant is sitting there. Find the total number of shortest paths that it can go along.
View SolutionThe area of a rectangular football field is 24200 sq.m. It is half as broad as it is long. What is the approx minimum distance a man will cover if he wishes to go from one corner to the opposite one?
View SolutionThe area of a rectangular football field is 24200 sq.m. It is half as broad as it is long. What is the approx minimum distance a man will cover if he wishes to go from one corner to the opposite one?
View Solution

