The four vertices of a unit square act as the centres of four quarter-circles. The arcs of these circles intersect each other within the square as depicted below. If the area of the region at the center of the square, which itself looks like a bloated square, is cordoned off by all the four arcs of circles is π3−√3+1, find the area of the shaded region.
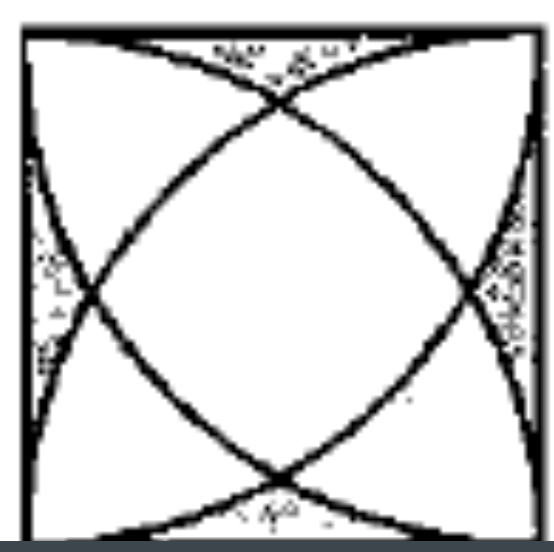
A) 4√3−2π3
B) 4−2√3−2π3
C) 4−√3−π3
D) none of these
The correct Answer is:A
Step by step video & image solution for The four vertices of a unit square act as the centres of four quarter-circles. The arcs of these circles intersect each other within the square as depicted below. If the area of the region at the center of the square, which itself looks like a bloated square, is cordoned off by all the four arcs of circles is pi/3 - sqrt3 + 1, find the area of the shaded region. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure , a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, find the area of the shaded region
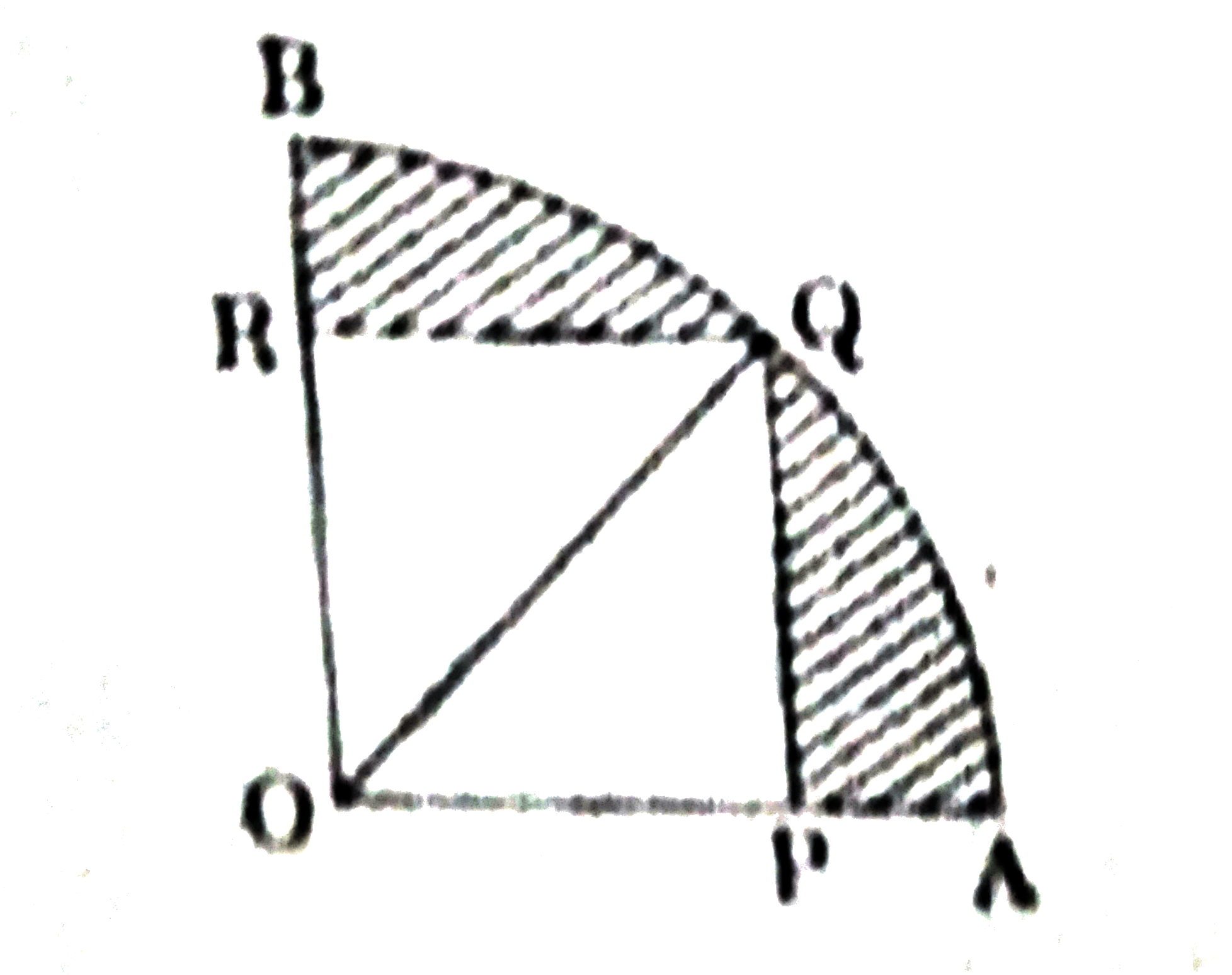
View SolutionIn Figure-9, a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, Find the area of the shaded region.
View Solution
Knowledge Check
The four corners are circle quadrants and at the centre there is a circle. The area of shaded region is
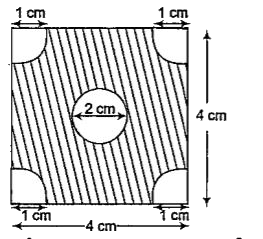 A(16−π)cm2B(16−2π)cm2C(16−2π)m2DNone of these
A(16−π)cm2B(16−2π)cm2C(16−2π)m2DNone of theseThe four corners are circle quadrants and at the centre there is a circle. The area of shaded region is
 A(16−π)cm2B(16−2π)cm2C(16−2π)m2DNone of these
A(16−π)cm2B(16−2π)cm2C(16−2π)m2DNone of theseIn the figure given below ABCD is a square of side 5 cm and all the four circles are of equal radius. What is the area of the shaded region ?
 A254(4−π)sq.cmB94(4−π)sq.cmC14(8−π)sq.cmDNone of these
A254(4−π)sq.cmB94(4−π)sq.cmC14(8−π)sq.cmDNone of these
In Fig 1, a square of diagonal 8 cm is inserted in a circle. Find the area ol the shaded region.

View SolutionIn figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.

View SolutionIn the given figure, a circle is inscribed in a square ABCD of side 28 cm. Find the area of the shaded region.
View SolutionO is the centre of a circle of diameter 4 cm and OABC the square, if the shaded area is 1/3 area of the square then the side of the square is
View SolutionThe given figure shows a circle inscribed in a square of side 14 cm.

What is the area of the shaded region?
View Solution
