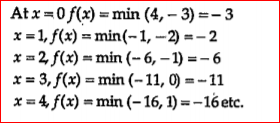What is the maximum value f(x)=min (4−5x,x−3) for every x∈(0,4)?
Video Solution
Text Solution
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
What is the maximum value of the function y = min (12−x,8+x)?
A12B10C11D8 - Question 2 - Select One
Manimum value of f(x)=3x2−4x+5 is
A−113B113C311D−311
The maximum value of 3cosx+4sinx+5 is
View SolutionThe absolute maximum value of f(x)=53x4+8x3−18x2+60
View SolutionLet f(x)=2−|x−3|,1≤x≤5 and for rest of the values f(x) can be obtained by using the relation f(5x)=αf(x)∀x∈R The maximum value of f(x) in [54,55] for α=2 is
View SolutionFind the maximum value of
f(x)=403x4+8x3−18x2+60View SolutionLet f(x)=∣∣x2−3x−4∣∣,−1≤x≤4 Then f(x) is monotonically increasing in [−1,32] f(x) monotonically decreasing in (32,4) the maximum value of f(x)is254 the minimum value of f(x) is 0
View SolutionFind the maximum value of the function f(x)=x−4e−2x, x>0
View Solution