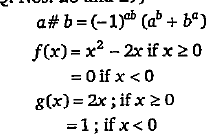
Find the value of f(g(2#3)+g(f(1#2) :
9401
1049
1094
none of these
The correct Answer is:C
Step by step video & image solution for Find the value of f(g(2#3)+g(f(1#2) : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
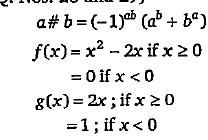
Find the value of f(2#3)#g(3#4) :
View SolutionIf f(g(x))=g(f(x))=x for all real numbers x, and f(2)=5 and f(5)=3, then the value of g(3)+g(f(2)) is
View SolutionIf two real functions f and g such that f(x)=x2 and g(x)=[x], then the value of f(−2)+g(−12) is
View SolutionFind the value of f2(4)+g2(4),iff'(x)=g(x)andg'(x)=−f(x) for all xandff(2)=4=f'(2).
View SolutionIf f(a,b)=a+b2
g(a,b)=a2+b2
h(a,b)=max (a,b)
Find the value of f(g(3,9)),h(−1,1)
View SolutionGiven a funtion g, continous everywhere such that g(1)=5and∫10g(t)dt=2. If f(x)=12∫x0(x−t)2g(t)dt, then find the value of f''(1)+f''(1).
View SolutionIf f(x)=x2g(x)andg(1)=6,g'(x)3, find the value of f' (1).
View SolutionIf f be a greatest integer function and g be an absolute value function, find the value of (f∘g)(−32)+(g∘f)(43).
View SolutionIf f, g, h are real functions defined by f=√x+1, g(x)=1x and h(x)=2x2−3, then find the values of (2fg+g−h)(1) and (2f+g−h)(1).
View SolutionQ.5 If f(g(x))=g(f(x))=x for all real numbers x, and f(2)=5 and f(5)=3, then the value g(3)+g(f(2)) is
View Solution
