In the following graph for x∈[−1,1],f(x) is defined by :
![In the following graph for x in [-1, 1], f(x) is defined by :](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_QNT_APT_CAT_C17_E04_107_Q01.png)
|x|+1
−|x|+1
−|x+1|
−|x|−1
The correct Answer is:B
Step by step video & image solution for In the following graph for x in [-1, 1], f(x) is defined by : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If the function f:[1,∞)→[1,∞) is defined by f(x) = 2x(x−1) is invertible, then f−1(x) is
A(12)x(x−1)B12(1+√1+4log2x)C12(1−√1+4log2x)Dnot definedIf the function f :[1,∞)→[1,∞) is defined by f(x)=2x(x−1), then f−1 (x) is
A(12)x(x−1)B12(1+√1+4log2x)C12(1−√1+4log2x)Dnot definedIn each of the following questions a pair of graphs f(x) and g(x) is given, defined for every x∈(−1,1). Choose the correct answer as
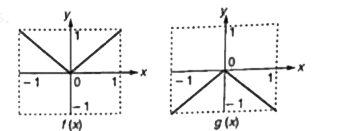 AA, if f(x)=−g(x) for every xBB. if f(x)=g(x) for x<0andf(x)=−g(x)x>0CC. if f(x)=−g(x) for x<0andf(x)=g(x),x>0DD. none of these
AA, if f(x)=−g(x) for every xBB. if f(x)=g(x) for x<0andf(x)=−g(x)x>0CC. if f(x)=−g(x) for x<0andf(x)=g(x),x>0DD. none of these
Which of the following statement are true for the function f defined for −1≤x≤3 in the figure limx→−1+f(x)=1
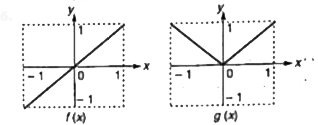
View SolutionIn each of the following questions a pair of graphs f(x) and g(x) is given, defined for every x∈(−1,1). Choose the correct answer as
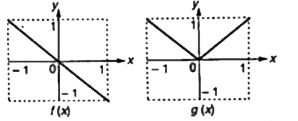
View SolutionIn each of the following questions a pair of graphs f(x) and g(x) is given, defined for every x∈(−1,1). Choose the correct answer as
View SolutionIf graph of a function f(x) which is defined in [-1, 4] is shown in the following figure then identify the correct statement(s).
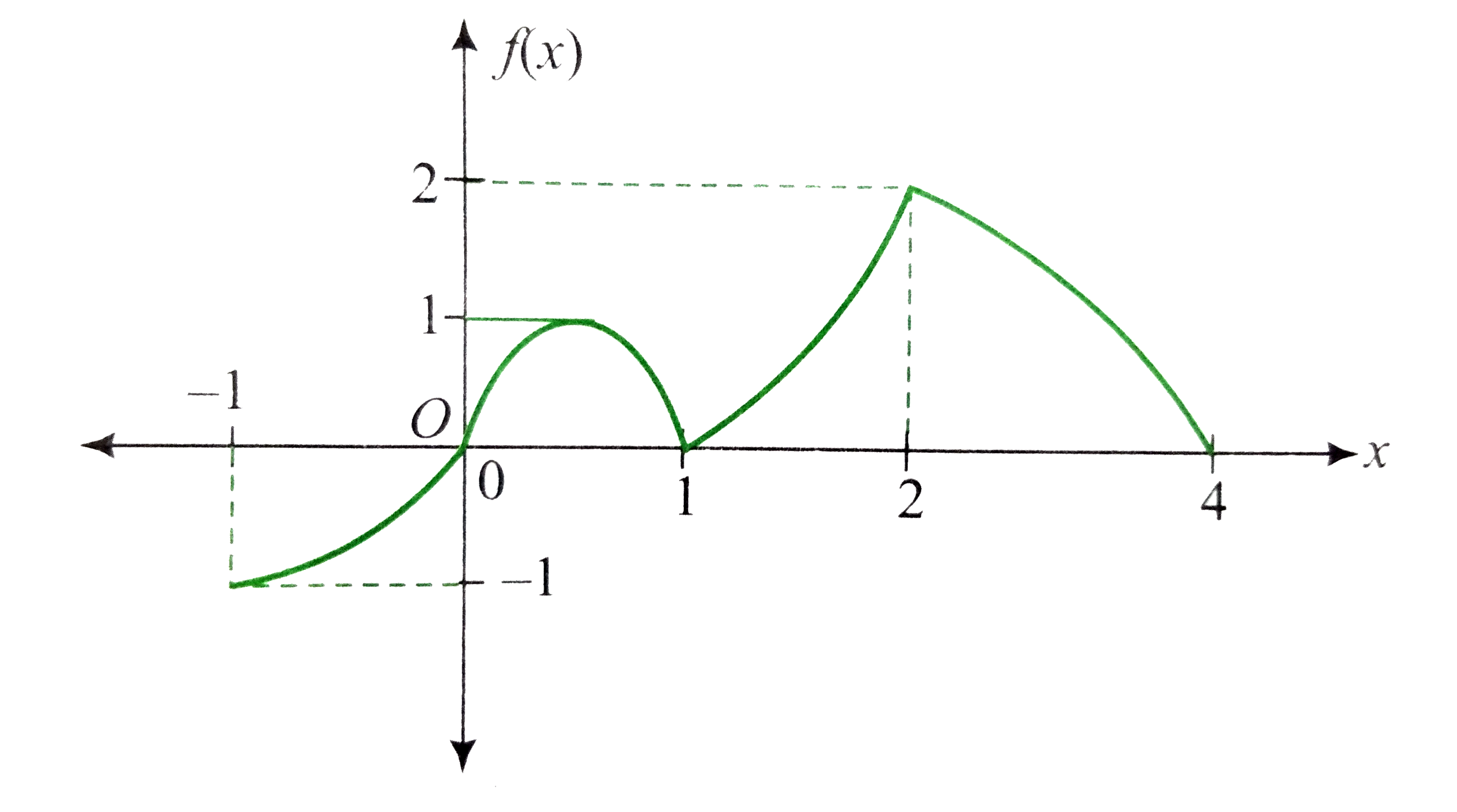
View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1) then f−1 is
View Solution
